
Rendleman-Bartter model
Encyclopedia
The Rendleman-Bartter model (Richard J. Rendleman, Jr. and Brit J. Bartter) in finance
is a short rate model
describing the evolution of interest rates. It is a "one factor model" as it describes interest rate movements as driven by only one source of market risk
. It can be used in the valuation of interest rate derivative
s. It is a stochastic asset model.
The model specifies that the instantaneous interest rate follows a geometric Brownian motion
:

where Wt is a Wiener process
modelling the random market risk factor. The drift parameter,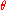 , represents a constant expected instantaneous rate of change in the interest rate, while the standard deviation
, represents a constant expected instantaneous rate of change in the interest rate, while the standard deviation
parameter, , determines the volatility
, determines the volatility
of the interest rate.
This is one of the early models of the short term interest rates, using the same stochastic process
as the one already used to describe the dynamics of the underlying price in stock options. Its main disadvantage is that it does not capture the mean reversion
of interest rates (their tendency to revert toward some value or range of values rather than wander without bounds in either direction).
Note that in 1979 Rendleman-Bartter also published a version of the Binomial options pricing model
. ("Two-State Option Pricing". Journal of Finance 24: 1093-1110.)
Mathematical finance
Mathematical finance is a field of applied mathematics, concerned with financial markets. The subject has a close relationship with the discipline of financial economics, which is concerned with much of the underlying theory. Generally, mathematical finance will derive and extend the mathematical...
is a short rate model
Short rate model
In the context of interest rate derivatives, a short-rate model is a mathematical model that describes the future evolution of interest rates by describing the future evolution of the short rate, usually written r_t \,.-The short rate:...
describing the evolution of interest rates. It is a "one factor model" as it describes interest rate movements as driven by only one source of market risk
Market risk
Market risk is the risk that the value of a portfolio, either an investment portfolio or a trading portfolio, will decrease due to the change in value of the market risk factors. The four standard market risk factors are stock prices, interest rates, foreign exchange rates, and commodity prices...
. It can be used in the valuation of interest rate derivative
Interest rate derivative
An interest rate derivative is a derivative where the underlying asset is the right to pay or receive a notional amount of money at a given interest rate...
s. It is a stochastic asset model.
The model specifies that the instantaneous interest rate follows a geometric Brownian motion
Geometric Brownian motion
A geometric Brownian motion is a continuous-time stochastic process in which the logarithm of the randomly varying quantity follows a Brownian motion, also called a Wiener process...
:

where Wt is a Wiener process
Wiener process
In mathematics, the Wiener process is a continuous-time stochastic process named in honor of Norbert Wiener. It is often called standard Brownian motion, after Robert Brown...
modelling the random market risk factor. The drift parameter,
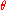 , represents a constant expected instantaneous rate of change in the interest rate, while the standard deviation
, represents a constant expected instantaneous rate of change in the interest rate, while the standard deviationStandard deviation
Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
parameter,
 , determines the volatility
, determines the volatilityVolatility (finance)
In finance, volatility is a measure for variation of price of a financial instrument over time. Historic volatility is derived from time series of past market prices...
of the interest rate.
This is one of the early models of the short term interest rates, using the same stochastic process
Stochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
as the one already used to describe the dynamics of the underlying price in stock options. Its main disadvantage is that it does not capture the mean reversion
Mean reversion
Mean reversion is a mathematical concept sometimes used for stock investing, but it can be applied to other assets. In general terms, the essence of the concept is the assumption that both a stock's high and low prices are temporary and that a stock's price will tend to move to the average price...
of interest rates (their tendency to revert toward some value or range of values rather than wander without bounds in either direction).
Note that in 1979 Rendleman-Bartter also published a version of the Binomial options pricing model
Binomial options pricing model
In finance, the binomial options pricing model provides a generalizable numerical method for the valuation of options. The binomial model was first proposed by Cox, Ross and Rubinstein in 1979. Essentially, the model uses a “discrete-time” model of the varying price over time of the underlying...
. ("Two-State Option Pricing". Journal of Finance 24: 1093-1110.)

