
Rellich-Kondrachov theorem
Encyclopedia
In mathematics
, the Rellich-Kondrachov theorem is a compact embedding
theorem
concerning Sobolev space
s. It is named after the Italian
-Austria
n mathematician
Franz Rellich
and the Russian mathematician Vladimir Iosifovich Kondrashov.
, bounded
Lipschitz domain
, and let 1 ≤ p < n. Set
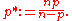
Then the Sobolev space W1,p(Ω; R) is continuously embedded
in the Lp space
Lp∗(Ω; R) and is compactly embedded
in Lq(Ω; R) for every 1 ≤ q < p∗. In symbols,

and
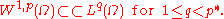
the inclusion (identity) operator is a compact operator
, the Rellich-Kondrachov theorem implies that any uniformly bounded sequence in W1,p(Ω; R) has a subsequence that converges in Lq(Ω; R). Stated in this form, the result is sometimes known as the Rellich-Kondrachov selection theorem (since one "selects" a convergent subsequence).
The Rellich-Kondrachov theorem may be used to prove the Poincaré inequality
, which states that for u ∈ W1,p(Ω; R) (where Ω satisfies the same hypotheses as above),
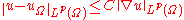
for some constant C depending only on p and the geometry of the domain Ω, where
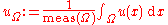
denotes the mean value of u over Ω.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Rellich-Kondrachov theorem is a compact embedding
Compactly embedded
In mathematics, the notion of being compactly embedded expresses the idea that one set or space is "well contained" inside another. There are versions of this concept appropriate to general topology and functional analysis.-Definition :...
theorem
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
concerning Sobolev space
Sobolev space
In mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function itself as well as its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, thus a Banach space...
s. It is named after the Italian
Italy
Italy , officially the Italian Republic languages]] under the European Charter for Regional or Minority Languages. In each of these, Italy's official name is as follows:;;;;;;;;), is a unitary parliamentary republic in South-Central Europe. To the north it borders France, Switzerland, Austria and...
-Austria
Austria
Austria , officially the Republic of Austria , is a landlocked country of roughly 8.4 million people in Central Europe. It is bordered by the Czech Republic and Germany to the north, Slovakia and Hungary to the east, Slovenia and Italy to the south, and Switzerland and Liechtenstein to the...
n mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Franz Rellich
Franz Rellich
Franz Rellich was an Austrian-Italian mathematician.He made important contributions in mathematical physics, in particular for the foundations of quantum mechanics and for the theory ofpartial differential equations....
and the Russian mathematician Vladimir Iosifovich Kondrashov.
Statement of the theorem
Let Ω ⊆ Rn be an openOpen set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
, bounded
Bounded set
In mathematical analysis and related areas of mathematics, a set is called bounded, if it is, in a certain sense, of finite size. Conversely, a set which is not bounded is called unbounded...
Lipschitz domain
Lipschitz domain
In mathematics, a Lipschitz domain is a domain in Euclidean space whose boundary is "sufficiently regular" in the sense that it can be thought of as locally being the graph of a Lipschitz continuous function...
, and let 1 ≤ p < n. Set
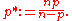
Then the Sobolev space W1,p(Ω; R) is continuously embedded
Continuously embedded
In mathematics, one normed vector space is said to be continuously embedded in another normed vector space if the inclusion function between them is continuous. In some sense, the two norms are "almost equivalent", even though they are not both defined on the same space...
in the Lp space
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
Lp∗(Ω; R) and is compactly embedded
Compactly embedded
In mathematics, the notion of being compactly embedded expresses the idea that one set or space is "well contained" inside another. There are versions of this concept appropriate to general topology and functional analysis.-Definition :...
in Lq(Ω; R) for every 1 ≤ q < p∗. In symbols,

and
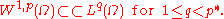
Consequences
Since an embedding is compact if and only ifIf and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
the inclusion (identity) operator is a compact operator
Compact operator
In functional analysis, a branch of mathematics, a compact operator is a linear operator L from a Banach space X to another Banach space Y, such that the image under L of any bounded subset of X is a relatively compact subset of Y...
, the Rellich-Kondrachov theorem implies that any uniformly bounded sequence in W1,p(Ω; R) has a subsequence that converges in Lq(Ω; R). Stated in this form, the result is sometimes known as the Rellich-Kondrachov selection theorem (since one "selects" a convergent subsequence).
The Rellich-Kondrachov theorem may be used to prove the Poincaré inequality
Poincaré inequality
In mathematics, the Poincaré inequality is a result in the theory of Sobolev spaces, named after the French mathematician Henri Poincaré. The inequality allows one to obtain bounds on a function using bounds on its derivatives and the geometry of its domain of definition. Such bounds are of great...
, which states that for u ∈ W1,p(Ω; R) (where Ω satisfies the same hypotheses as above),
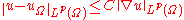
for some constant C depending only on p and the geometry of the domain Ω, where
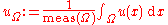
denotes the mean value of u over Ω.

