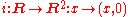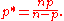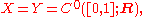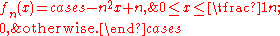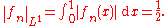In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, one normed vector space

Normed vector space

In mathematics, with 2- or 3-dimensional vectors with real-valued entries, the idea of the "length" of a vector is intuitive and can easily be extended to any real vector space Rn. The following properties of "vector length" are crucial....

 is said to be continuously embedded in another normed vector space if the inclusion function between them is continuous

Continuous function

In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...

. In some sense, the two norms are "almost equivalent", even though they are not both defined on the same space. Several of the Sobolev embedding theorems

Sobolev inequality

In mathematics, there is in mathematical analysis a class of Sobolev inequalities, relating norms including those of Sobolev spaces. These are used to prove the Sobolev embedding theorem, giving inclusions between certain Sobolev spaces, and the Rellich–Kondrachov theorem showing that under...

 are continuous embedding theorems.

Definition

Let X and Y be two normed vector spaces, with norms ||·||_X and ||·||_Y respectively, such that X ⊆ Y. If the inclusion map (identity function)

Identity function

In mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...

is continuous, i.e. if there exists a constant C ≥ 0 such that


for every x in X, then X is said to be continuously embedded in Y. Some authors use the hooked arrow “↪” to denote a continuous embedding, i.e. “X ↪ Y” means “X and Y are normed spaces with X continuously embedded in Y”. This is a consistent use of notation from the point of view of the category of topological vector spaces

Category of topological vector spaces

In mathematics, the category of topological vector spaces is the category whose objects are topological vector spaces and whose morphisms are continuous linear maps between them. This is a category because the composition of two continuous linear maps is again continuous...

, in which the morphism

Morphism

In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...

s (“arrows”) are the continuous linear maps.

Examples

• A finite-dimensional example of a continuous embedding is given by a natural embedding of the real line
  Real line
  In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
  
   X = R into the plane Y = R², where both spaces are given the Euclidean norm:

In this case, ||x||_X = ||x||_Y for every real number X. Clearly, the optimal choice of constant C is C = 1.

• An infinite-dimensional example of a continuous embedding is given by the Rellich-Kondrachov theorem
  Rellich-Kondrachov theorem
  In mathematics, the Rellich-Kondrachov theorem is a compact embedding theorem concerning Sobolev spaces. It is named after the Italian-Austrian mathematician Franz Rellich and the Russian mathematician Vladimir Iosifovich Kondrashov.-Statement of the theorem:...
  
  : let Ω ⊆ Rⁿ be an open
  Open set
  The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
  
  , bounded
  Bounded set
  In mathematical analysis and related areas of mathematics, a set is called bounded, if it is, in a certain sense, of finite size. Conversely, a set which is not bounded is called unbounded...
  
  , Lipschitz domain
  Lipschitz domain
  In mathematics, a Lipschitz domain is a domain in Euclidean space whose boundary is "sufficiently regular" in the sense that it can be thought of as locally being the graph of a Lipschitz continuous function...
  
  , and let 1 ≤ p < n. Set

Then the Sobolev space W^1,p(Ω; R) is continuously embedded in the L^p space

Lp space

In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...

 L^p∗(Ω; R). In fact, for 1 ≤ q < p^∗, this embedding is compact

Compactly embedded

In mathematics, the notion of being compactly embedded expresses the idea that one set or space is "well contained" inside another. There are versions of this concept appropriate to general topology and functional analysis.-Definition :...

. The optimal constant C will depend upon the geometry of the domain Ω.

• Infinite-dimensional spaces also offer examples of discontinuous embeddings. For example, consider

the space of continuous real-valued functions defined on the unit interval, but equip X with the L¹ norm and Y with the supremum norm. For n ∈ N, let f_n be the continuous

Continuous function

In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...

, piecewise linear function given by

Then, for every n, ||f_n||_Y = ||f_n||_∞ = n, but

Hence, no constant C can be found such that ||f_n||_Y ≤ C||f_n||_X, and so the embedding of X into Y is discontinuous.