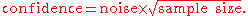Relative risk
Encyclopedia
In statistics
and mathematical epidemiology
, relative risk (RR) is the risk of an event (or of developing a disease) relative to exposure. Relative risk is a ratio
of the probability
of the event occurring in the exposed group versus a non-exposed group.

Consider an example where the probability
of developing lung cancer among smokers was 20% and among non-smokers 1%. This situation is expressed in the 2 × 2 table to the right.
Here, a = 20, b = 80, c = 1, and d = 99. Then the relative risk of cancer associated with smoking would be
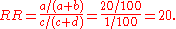
Smokers would be twenty times as likely as non-smokers to develop lung cancer.
Another term for the relative risk is the risk ratio because it is the ratio of the risk in the exposed divided by the risk in the unexposed.
data, where it is used to compare the risk of developing a disease, in people not receiving the new medical treatment (or receiving a placebo) versus people who are receiving an established (standard of care) treatment. Alternatively, it is used to compare the risk of developing a side effect in people receiving a drug as compared to the people who are not receiving the treatment (or receiving a placebo). It is particularly attractive because it can be calculated by hand in the simple case, but is also amenable to regression modelling
, typically in a Poisson regression
framework.
In a simple comparison between an experimental group and a control group:
As a consequence of the Delta method, the log
of the relative risk has a sampling distribution that is approximately normal with variance that can be estimated by a formula involving the number of subjects in each group and the event rates in each group (see Delta method). This permits the construction of a confidence interval
(CI) which is symmetric around log(RR), i.e.,
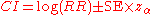
where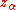 is the standard score
is the standard score
for the chosen level of significance
and SE the standard error
. The antilog can be taken of the two bounds of the log-CI, giving the high and low bounds for an asymmetric confidence interval around the relative risk.
In regression models, the treatment is typically included as a dummy variable along with other factors that may affect risk. The relative risk is normally reported as calculated for the mean
of the sample values of the explanatory variables.
, although it asymptotically approaches it for small probabilities. In the example of association of smoking to lung cancer considered above, if a is substantially smaller than b, then a/(a + b) a/b. And if similarly c is much smaller than d, then c/(c + d)
a/b. And if similarly c is much smaller than d, then c/(c + d)  c/d. Thus
c/d. Thus
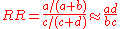
This is the odds ratio.
In fact, the odds ratio has much wider use in statistics, since logistic regression
, often associated with clinical trial
s, works with the log of the odds ratio, not relative risk. Because the log of the odds ratio is estimated as a linear function of the explanatory variables, the estimated odds ratio for 70-year-olds and 60-year-olds associated with type of treatment would be the same in a logistic regression models where the outcome is associated with drug and age, although the relative risk might be significantly different. In cases like this, statistical models of the odds ratio often reflect the underlying mechanisms more effectively.
Since relative risk is a more intuitive measure of effectiveness, the distinction is important especially in cases of medium to high probabilities. If action A carries a risk of 99.9% and action B a risk of 99.0% then the relative risk is just over 1, while the odds associated with action A are almost 10 times higher than the odds with B.
In medical research, the odds ratio
is commonly used for case-control studies, as odds, but not probabilities, are usually estimated. Relative risk is used in randomized controlled trial
s and cohort studies
.
In statistical modelling, approaches like poisson regression
(for counts of events per unit exposure) have relative risk interpretations: the estimated effect of an explanatory variable is multiplicative on the rate, and thus leads to a risk ratio or relative risk. Logistic regression
(for binary outcomes, or counts of successes out of a number of trials) must be interpreted in odds-ratio terms: the effect of an explanatory variable is multiplicative on the odds and thus leads to an odds ratio.
is dependent on the relative difference between the conditions compared, the amount of measurement and the noise associated with the measurement (of the events considered). In other words, the confidence one has, in a given relative risk being non-random (i.e. it is not a consequence of chance
), depends on the signal-to-noise ratio
and the sample size.
Expressed mathematically, the confidence that a result is not by random chance is given by the following formula by Sackett
:
For clarity, the above formula is presented in tabular form below.
Dependence of confidence with noise, signal and sample size (tabular form)
In words, the confidence is higher if the noise is lower and/or the sample size is larger and/or the effect size (signal) is increased. The confidence of a relative risk value (and its associated confidence interval) is not dependent on effect size alone. If the sample size is large and the noise is low a small effect size can be measured with great confidence. Whether a small effect size is considered important is dependent on the context of the events compared.
In medicine, small effect sizes (reflected by small relative risk values) are usually considered clinically relevant (if there is great confidence in them) and are frequently used to guide treatment decisions. A relative risk of 1.10 may seem very small, but over a large number of patients will make a noticeable difference. Whether a given treatment is considered a worthy endeavour is dependent on the risks, benefits and costs.
The distribution of the log Relative Risk is approximately normal with:
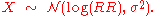
The standard error
for the log (Relative Risk) is approximately:
SE(log(RR)) = sqrt( [1/a + 1/c] - [1/(a+b) + 1/(c+d)] )
This is an asymptotic approximation.
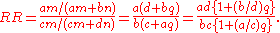
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
and mathematical epidemiology
Epidemiology
Epidemiology is the study of health-event, health-characteristic, or health-determinant patterns in a population. It is the cornerstone method of public health research, and helps inform policy decisions and evidence-based medicine by identifying risk factors for disease and targets for preventive...
, relative risk (RR) is the risk of an event (or of developing a disease) relative to exposure. Relative risk is a ratio
Ratio
In mathematics, a ratio is a relationship between two numbers of the same kind , usually expressed as "a to b" or a:b, sometimes expressed arithmetically as a dimensionless quotient of the two which explicitly indicates how many times the first number contains the second In mathematics, a ratio is...
of the probability
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
of the event occurring in the exposed group versus a non-exposed group.

Consider an example where the probability
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
of developing lung cancer among smokers was 20% and among non-smokers 1%. This situation is expressed in the 2 × 2 table to the right.
| Risk | Disease status | |
|---|---|---|
| Present | Absent | |
| Smoker |  |
 |
| Non-smoker |  |
 |
Here, a = 20, b = 80, c = 1, and d = 99. Then the relative risk of cancer associated with smoking would be
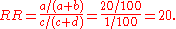
Smokers would be twenty times as likely as non-smokers to develop lung cancer.
Another term for the relative risk is the risk ratio because it is the ratio of the risk in the exposed divided by the risk in the unexposed.
Statistical use and meaning
Relative risk is used frequently in the statistical analysis of binary outcomes where the outcome of interest has relatively low probability. It is thus often suited to clinical trialClinical trial
Clinical trials are a set of procedures in medical research and drug development that are conducted to allow safety and efficacy data to be collected for health interventions...
data, where it is used to compare the risk of developing a disease, in people not receiving the new medical treatment (or receiving a placebo) versus people who are receiving an established (standard of care) treatment. Alternatively, it is used to compare the risk of developing a side effect in people receiving a drug as compared to the people who are not receiving the treatment (or receiving a placebo). It is particularly attractive because it can be calculated by hand in the simple case, but is also amenable to regression modelling
Regression analysis
In statistics, regression analysis includes many techniques for modeling and analyzing several variables, when the focus is on the relationship between a dependent variable and one or more independent variables...
, typically in a Poisson regression
Poisson regression
In statistics, Poisson regression is a form of regression analysis used to model count data and contingency tables. Poisson regression assumes the response variable Y has a Poisson distribution, and assumes the logarithm of its expected value can be modeled by a linear combination of unknown...
framework.
In a simple comparison between an experimental group and a control group:
- A relative risk of 1 means there is no difference in risk between the two groups.
- An RR of < 1 means the event is less likely to occur in the experimental group than in the control group.
- An RR of > 1 means the event is more likely to occur in the experimental group than in the control group.
As a consequence of the Delta method, the log
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
of the relative risk has a sampling distribution that is approximately normal with variance that can be estimated by a formula involving the number of subjects in each group and the event rates in each group (see Delta method). This permits the construction of a confidence interval
Confidence interval
In statistics, a confidence interval is a particular kind of interval estimate of a population parameter and is used to indicate the reliability of an estimate. It is an observed interval , in principle different from sample to sample, that frequently includes the parameter of interest, if the...
(CI) which is symmetric around log(RR), i.e.,
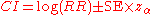
where
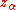 is the standard score
is the standard scoreStandard score
In statistics, a standard score indicates how many standard deviations an observation or datum is above or below the mean. It is a dimensionless quantity derived by subtracting the population mean from an individual raw score and then dividing the difference by the population standard deviation...
for the chosen level of significance
Statistical significance
In statistics, a result is called statistically significant if it is unlikely to have occurred by chance. The phrase test of significance was coined by Ronald Fisher....
and SE the standard error
Standard error (statistics)
The standard error is the standard deviation of the sampling distribution of a statistic. The term may also be used to refer to an estimate of that standard deviation, derived from a particular sample used to compute the estimate....
. The antilog can be taken of the two bounds of the log-CI, giving the high and low bounds for an asymmetric confidence interval around the relative risk.
In regression models, the treatment is typically included as a dummy variable along with other factors that may affect risk. The relative risk is normally reported as calculated for the mean
Mean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
of the sample values of the explanatory variables.
Association with odds ratio
Relative risk is different from the odds ratioOdds ratio
The odds ratio is a measure of effect size, describing the strength of association or non-independence between two binary data values. It is used as a descriptive statistic, and plays an important role in logistic regression...
, although it asymptotically approaches it for small probabilities. In the example of association of smoking to lung cancer considered above, if a is substantially smaller than b, then a/(a + b)
 a/b. And if similarly c is much smaller than d, then c/(c + d)
a/b. And if similarly c is much smaller than d, then c/(c + d)  c/d. Thus
c/d. Thus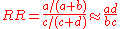
This is the odds ratio.
In fact, the odds ratio has much wider use in statistics, since logistic regression
Logistic regression
In statistics, logistic regression is used for prediction of the probability of occurrence of an event by fitting data to a logit function logistic curve. It is a generalized linear model used for binomial regression...
, often associated with clinical trial
Clinical trial
Clinical trials are a set of procedures in medical research and drug development that are conducted to allow safety and efficacy data to be collected for health interventions...
s, works with the log of the odds ratio, not relative risk. Because the log of the odds ratio is estimated as a linear function of the explanatory variables, the estimated odds ratio for 70-year-olds and 60-year-olds associated with type of treatment would be the same in a logistic regression models where the outcome is associated with drug and age, although the relative risk might be significantly different. In cases like this, statistical models of the odds ratio often reflect the underlying mechanisms more effectively.
Since relative risk is a more intuitive measure of effectiveness, the distinction is important especially in cases of medium to high probabilities. If action A carries a risk of 99.9% and action B a risk of 99.0% then the relative risk is just over 1, while the odds associated with action A are almost 10 times higher than the odds with B.
In medical research, the odds ratio
Odds ratio
The odds ratio is a measure of effect size, describing the strength of association or non-independence between two binary data values. It is used as a descriptive statistic, and plays an important role in logistic regression...
is commonly used for case-control studies, as odds, but not probabilities, are usually estimated. Relative risk is used in randomized controlled trial
Randomized controlled trial
A randomized controlled trial is a type of scientific experiment - a form of clinical trial - most commonly used in testing the safety and efficacy or effectiveness of healthcare services or health technologies A randomized controlled trial (RCT) is a type of scientific experiment - a form of...
s and cohort studies
Cohort study
A cohort study or panel study is a form of longitudinal study used in medicine, social science, actuarial science, and ecology. It is an analysis of risk factors and follows a group of people who do not have the disease, and uses correlations to determine the absolute risk of subject contraction...
.
In statistical modelling, approaches like poisson regression
Poisson regression
In statistics, Poisson regression is a form of regression analysis used to model count data and contingency tables. Poisson regression assumes the response variable Y has a Poisson distribution, and assumes the logarithm of its expected value can be modeled by a linear combination of unknown...
(for counts of events per unit exposure) have relative risk interpretations: the estimated effect of an explanatory variable is multiplicative on the rate, and thus leads to a risk ratio or relative risk. Logistic regression
Logistic regression
In statistics, logistic regression is used for prediction of the probability of occurrence of an event by fitting data to a logit function logistic curve. It is a generalized linear model used for binomial regression...
(for binary outcomes, or counts of successes out of a number of trials) must be interpreted in odds-ratio terms: the effect of an explanatory variable is multiplicative on the odds and thus leads to an odds ratio.
Statistical significance (confidence) and relative risk
Whether a given relative risk can be considered statistically significantStatistical significance
In statistics, a result is called statistically significant if it is unlikely to have occurred by chance. The phrase test of significance was coined by Ronald Fisher....
is dependent on the relative difference between the conditions compared, the amount of measurement and the noise associated with the measurement (of the events considered). In other words, the confidence one has, in a given relative risk being non-random (i.e. it is not a consequence of chance
Randomness
Randomness has somewhat differing meanings as used in various fields. It also has common meanings which are connected to the notion of predictability of events....
), depends on the signal-to-noise ratio
Signal-to-noise ratio
Signal-to-noise ratio is a measure used in science and engineering that compares the level of a desired signal to the level of background noise. It is defined as the ratio of signal power to the noise power. A ratio higher than 1:1 indicates more signal than noise...
and the sample size.
Expressed mathematically, the confidence that a result is not by random chance is given by the following formula by Sackett
David Sackett
David Lawrence Sackett, OC, FRSC is a Canadian medical doctor and a pioneer in evidence-based medicine. He founded the first department of clinical epidemiology in Canada at McMaster University, and the Oxford Centre for Evidence-Based Medicine...
:
For clarity, the above formula is presented in tabular form below.
Dependence of confidence with noise, signal and sample size (tabular form)
| Parameter | Parameter increases | Parameter decreases |
|---|---|---|
| Noise | Confidence decreases | Confidence increases |
| Signal | Confidence increases | Confidence decreases |
| Sample size | Confidence increases | Confidence decreases |
In words, the confidence is higher if the noise is lower and/or the sample size is larger and/or the effect size (signal) is increased. The confidence of a relative risk value (and its associated confidence interval) is not dependent on effect size alone. If the sample size is large and the noise is low a small effect size can be measured with great confidence. Whether a small effect size is considered important is dependent on the context of the events compared.
In medicine, small effect sizes (reflected by small relative risk values) are usually considered clinically relevant (if there is great confidence in them) and are frequently used to guide treatment decisions. A relative risk of 1.10 may seem very small, but over a large number of patients will make a noticeable difference. Whether a given treatment is considered a worthy endeavour is dependent on the risks, benefits and costs.
The distribution of the log Relative Risk is approximately normal with:
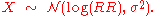
The standard error
Standard error (statistics)
The standard error is the standard deviation of the sampling distribution of a statistic. The term may also be used to refer to an estimate of that standard deviation, derived from a particular sample used to compute the estimate....
for the log (Relative Risk) is approximately:
SE(log(RR)) = sqrt( [1/a + 1/c] - [1/(a+b) + 1/(c+d)] )
This is an asymptotic approximation.
Worked example
- Example 3: Ratios are presented for each of experimental and control groups. In the disease-risk 2 × 2 table above, suppose a + c = 1 and b + d = 1 and the total number of patients and healthy people be m and n, respectively. Then prevalence ratio becomes p = m/(m + n). We can put q = m/n = p/(1 − p). Thus
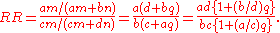
- If p is small enough, then q would be small enough and either of (b/d)q and (a/c)q would be small enough to be regarded as 0 compared with 1. RR would be reduced to the odd ratio as above.
- Among Japanese, not a small fraction of patients of Behçet's disease are bestowed with a specific HLA type, namely HLA-B51 gene. In a survey, the proportion is 63% of the patients with this gene, while in healthy people the ratio is 21%. If the figures are considered to be representative for most Japanese, using the values of 12,700 patients in Japan in 1984 and the Japanese population about 120 million in 1982, then RR = 6.40. Compare with the odd ratio 6.41.
See also
- Absolute risk reductionAbsolute risk reductionIn epidemiology, the absolute risk reduction or risk difference is the decrease in risk of a given activity or treatment in relation to a control activity or treatment. It is the inverse of the number needed to treat....
- (Population) attributable riskAttributable riskIn epidemiology, attributable risk is the difference in rate of a condition between an exposed population and an unexposed population.. Attributable risk is mostly calculated in cohort studies, where individuals are assembled on exposure status and followed over a period of time. Investigators...
- Confidence intervalConfidence intervalIn statistics, a confidence interval is a particular kind of interval estimate of a population parameter and is used to indicate the reliability of an estimate. It is an observed interval , in principle different from sample to sample, that frequently includes the parameter of interest, if the...
- Number needed to treatNumber needed to treatThe number needed to treat is an epidemiological measure used in assessing the effectiveness of a health-care intervention, typically a treatment with medication. The NNT is the average number of patients who need to be treated to prevent one additional bad outcome...
(NNT) - Number needed to harmNumber needed to harmThe number needed to harm is an epidemiological measure that indicates how many patients need to be exposed to a risk-factor over a specific period to cause harm in one patient that would not otherwise have been harmed. It is defined as the inverse of the attributable risk...
(NNH) - OpenEpiOpenEpiOpenEpi is a free, web-based, open source, operating system-independent series of programs for use in epidemiology, biostatistics, public health, and medicine, providing a number of epidemiologic and statistical tools for summary data. OpenEpi was developed in JavaScript and HTML, and can be run in...
- Epi InfoEpi InfoEpi Info is public domain statistical software for epidemiology developed by Centers for Disease Control and Prevention in Atlanta, Georgia ....
- The rare disease assumptionThe rare disease assumptionThe rare disease assumption is a useful mathematical assumption in epidemiologic case control studies where the hypothesis tests the association between an exposure and a disease. It is assumed that, if the prevalence of the disease is low, then the odds ratio approaches the relative risk.Case...
External links
- EBM glossary
- Odds ratio versus relative risk
- Odds Ratio vs. Relative Risk Medical University of South Carolina
- Relative risk online calculator