Refinement monoid
Encyclopedia
In mathematics
, a refinement monoid is a commutative monoid M such that for any elements a0, a1, b0, b1 of M such that a0+a1=b0+b1, there are elements c00, c01, c10, c11 of M such that a0=c00+c01, a1=c10+c11, b0=c00+c10, and b1=c01+c11.
A commutative monoid M is conical, if x+y=0 implies that x=y=0, for any elements x,y of M.
with zero is a refinement monoid if and only if it is distributive
.
Any abelian group
is a refinement monoid.
The positive cone
G+ of a partially ordered abelian group
G is a refinement monoid if and only if G is an interpolation group, the latter meaning that for any elements a0, a1, b0, b1 of G such that ai ≤ bj for all i, j<2, there exists an element x of G such that ai ≤ x ≤ bj for all i, j<2. This holds, for example, in case G is lattice-ordered
.
The isomorphism type of a Boolean algebra B is the class of all Boolean algebras isomorphic to B. (If we want this to be a set, restrict to Boolean algebras of set-theoretical rank below the one of B.)
The class of isomorphism types of Boolean algebras, endowed with the addition defined by
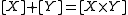(for any Boolean algebras X and Y, where 
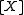denotes the isomorphism type of X), is a conical refinement monoid.
), or V-measure, if for all c in A and all x,y in M such that μ(c)=x+y, there are disjoint a, b in A such that c=a ∨ b, μ(a)=x, and μ(b)=y.
An element e in a commutative monoid M is measurable (with respect to M), if there are a Boolean algebra A and a V-measure μ : A → M such that μ(1)=e---we say that μ measures e. We say that M is measurable, if any element of M is measurable (with respect to M). Of course, every measurable monoid is a conical refinement monoid.
Hans Dobbertin
proved in 1983 that any conical refinement monoid with at most ℵ1 elements is measurable. He also proved that any element in an at most countable conical refinement monoid is measured by a unique (up to isomorphism) V-measure on a unique at most countable Boolean algebra.
He raised there the problem whether any conical refinement monoid is measurable. This was answered in the negative by Friedrich Wehrung in 1998. The counterexamples can have any cardinality greater than or equal to ℵ2.
(with unit) R, denote by FP(R) the class of finitely generated
projective
right R-modules. Equivalently, the objects of FP(R) are the direct summands of all modules of the form Rn, with n a positive integer, viewed as a right module over itself. Denote by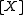
the isomorphism type of an object X in FP(R). Then the set V(R) of all isomorphism types of members of FP(R), endowed with the addition defined by 
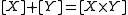, is a conical commutative monoid
. In addition, if R is von Neumann regular
, then V(R) is a refinement monoid. It has the order-unit
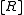. We say that V(R) encodes the nonstable K-theory of R.
For example, if R is a division ring
, then the members of FP(R) are exactly the finite-dimensional right vector spaces
over R, and two vector spaces are isomorphic if and only if they have the same dimension
. Hence V(R) is isomorphic to the monoid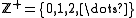
of all natural numbers, endowed with its usual addition.
A slightly more complicated example can be obtained as follows. A matricial algebra over a field
F is a finite product of rings of the form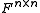
=ring of all square matrices
with n rows and entries in F, for variable positive integers n. A direct limit of matricial algebras over F is a locally matricial algebra over F. Every locally matricial algebra is von Neumann regular. For any locally matricial algebra R, V(R) is the positive cone
of a so-called dimension group. By definition, a dimension group is a partially ordered abelian group
whose underlying order is directed
, whose positive cone is a refinement monoid, and which is unperforated, the letter meaning that mx≥0 implies that x≥0, for any element x of G and any positive integer m. Any simplicial group, that is, a partially ordered abelian group of the form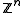
, is a dimension group. Effros, Handelman, and Shen proved in 1980 that dimension groups are exactly the direct limit
s of simplicial groups, where the transition maps are positive homomorphisms. This result had already been proved in 1976, in a slightly different form, by P.A. Grillet. Elliott proved in 1976 that the positive cone of any countable direct limit of simplicial groups is isomorphic to V(R), for some locally matricial ring R. Finally, Goodearl and Handelman proved in 1986 that the positive cone of any dimension group with at most ℵ1 elements is isomorphic to V(R), for some locally matricial ring R (over any given field).
Wehrung proved in 1998 that there are dimension groups with order-unit whose positive cone cannot be represented as V(R), for a von Neumann regular ring R. The given examples can have any cardinality greater than or equal to ℵ2. Whether any conical refinement monoid with at most ℵ1 (or even ℵ0) elements can be represented as V(R) for R von Neumann regular is an open problem.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a refinement monoid is a commutative monoid M such that for any elements a0, a1, b0, b1 of M such that a0+a1=b0+b1, there are elements c00, c01, c10, c11 of M such that a0=c00+c01, a1=c10+c11, b0=c00+c10, and b1=c01+c11.
A commutative monoid M is conical, if x+y=0 implies that x=y=0, for any elements x,y of M.
Basic examples
A join-semilatticeSemilattice
In mathematics, a join-semilattice is a partially ordered set which has a join for any nonempty finite subset. Dually, a meet-semilattice is a partially ordered set which has a meet for any nonempty finite subset...
with zero is a refinement monoid if and only if it is distributive
Distributivity (order theory)
In the mathematical area of order theory, there are various notions of the common concept of distributivity, applied to the formation of suprema and infima...
.
Any abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
is a refinement monoid.
The positive cone
Ordered group
In abstract algebra, a partially-ordered group is a group equipped with a partial order "≤" that is translation-invariant; in other words, "≤" has the property that, for all a, b, and g in G, if a ≤ b then a+g ≤ b+g and g+a ≤ g+b.An element x of G is called positive element if 0 ≤ x...
G+ of a partially ordered abelian group
Ordered group
In abstract algebra, a partially-ordered group is a group equipped with a partial order "≤" that is translation-invariant; in other words, "≤" has the property that, for all a, b, and g in G, if a ≤ b then a+g ≤ b+g and g+a ≤ g+b.An element x of G is called positive element if 0 ≤ x...
G is a refinement monoid if and only if G is an interpolation group, the latter meaning that for any elements a0, a1, b0, b1 of G such that ai ≤ bj for all i, j<2, there exists an element x of G such that ai ≤ x ≤ bj for all i, j<2. This holds, for example, in case G is lattice-ordered
Ordered group
In abstract algebra, a partially-ordered group is a group equipped with a partial order "≤" that is translation-invariant; in other words, "≤" has the property that, for all a, b, and g in G, if a ≤ b then a+g ≤ b+g and g+a ≤ g+b.An element x of G is called positive element if 0 ≤ x...
.
The isomorphism type of a Boolean algebra B is the class of all Boolean algebras isomorphic to B. (If we want this to be a set, restrict to Boolean algebras of set-theoretical rank below the one of B.)
The class of isomorphism types of Boolean algebras, endowed with the addition defined by
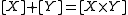(for any Boolean algebras X and Y, where 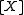denotes the isomorphism type of X), is a conical refinement monoid.Vaught measures on Boolean algebras
For a Boolean algebra A and a commutative monoid M, a map μ : A → M is a measure, if μ(a)=0 if and only if a=0, and μ(a ∨ b)=μ(a)+μ(b) whenever a and b are disjoint (that is, a ∧ b=0), for any a, b in A. We say in addition that μ is a Vaught measure (after Robert Lawson VaughtRobert Lawson Vaught
Robert Lawson Vaught was a mathematical logician, and one of the founders of model theory.-Life:Vaught was a bit of a musical prodigy in his youth, in his case the piano. He began his university studies at Pomona College, at age 16. When World War II broke out, he enlisted US Navy which assigned...
), or V-measure, if for all c in A and all x,y in M such that μ(c)=x+y, there are disjoint a, b in A such that c=a ∨ b, μ(a)=x, and μ(b)=y.
An element e in a commutative monoid M is measurable (with respect to M), if there are a Boolean algebra A and a V-measure μ : A → M such that μ(1)=e---we say that μ measures e. We say that M is measurable, if any element of M is measurable (with respect to M). Of course, every measurable monoid is a conical refinement monoid.
Hans Dobbertin
Hans Dobbertin
Hans Dobbertin, was a German cryptographer who is best known for his work on cryptanalysis of the MD4, MD5, and original RIPEMD hash functions, and for his part in the design of the new version of the RIPEMD hash function...
proved in 1983 that any conical refinement monoid with at most ℵ1 elements is measurable. He also proved that any element in an at most countable conical refinement monoid is measured by a unique (up to isomorphism) V-measure on a unique at most countable Boolean algebra.
He raised there the problem whether any conical refinement monoid is measurable. This was answered in the negative by Friedrich Wehrung in 1998. The counterexamples can have any cardinality greater than or equal to ℵ2.
Nonstable K-theory of von Neumann regular rings
For a ringRing (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
(with unit) R, denote by FP(R) the class of finitely generated
Finitely generated
In mathematics, finitely generated may refer to:* Finitely generated group* Finitely generated monoid* Finitely generated abelian group* Finitely generated module* Finitely generated ideal* Finitely generated algebra* Finitely generated space...
projective
Projective module
In mathematics, particularly in abstract algebra and homological algebra, the concept of projective module over a ring R is a more flexible generalisation of the idea of a free module...
right R-modules. Equivalently, the objects of FP(R) are the direct summands of all modules of the form Rn, with n a positive integer, viewed as a right module over itself. Denote by
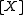the isomorphism type of an object X in FP(R). Then the set V(R) of all isomorphism types of members of FP(R), endowed with the addition defined by 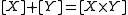, is a conical commutative monoidMonoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
. In addition, if R is von Neumann regular
Von Neumann regular ring
In mathematics, a von Neumann regular ring is a ring R such that for every a in R there exists an x in R withOne may think of x as a "weak inverse" of a...
, then V(R) is a refinement monoid. It has the order-unit
Monoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
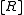. We say that V(R) encodes the nonstable K-theory of R.For example, if R is a division ring
Division ring
In abstract algebra, a division ring, also called a skew field, is a ring in which division is possible. Specifically, it is a non-trivial ring in which every non-zero element a has a multiplicative inverse, i.e., an element x with...
, then the members of FP(R) are exactly the finite-dimensional right vector spaces
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
over R, and two vector spaces are isomorphic if and only if they have the same dimension
Dimension (vector space)
In mathematics, the dimension of a vector space V is the cardinality of a basis of V. It is sometimes called Hamel dimension or algebraic dimension to distinguish it from other types of dimension...
. Hence V(R) is isomorphic to the monoid
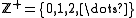of all natural numbers, endowed with its usual addition.A slightly more complicated example can be obtained as follows. A matricial algebra over a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
F is a finite product of rings of the form
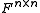=ring of all square matricesMatrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
with n rows and entries in F, for variable positive integers n. A direct limit of matricial algebras over F is a locally matricial algebra over F. Every locally matricial algebra is von Neumann regular. For any locally matricial algebra R, V(R) is the positive cone
Ordered group
In abstract algebra, a partially-ordered group is a group equipped with a partial order "≤" that is translation-invariant; in other words, "≤" has the property that, for all a, b, and g in G, if a ≤ b then a+g ≤ b+g and g+a ≤ g+b.An element x of G is called positive element if 0 ≤ x...
of a so-called dimension group. By definition, a dimension group is a partially ordered abelian group
Ordered group
In abstract algebra, a partially-ordered group is a group equipped with a partial order "≤" that is translation-invariant; in other words, "≤" has the property that, for all a, b, and g in G, if a ≤ b then a+g ≤ b+g and g+a ≤ g+b.An element x of G is called positive element if 0 ≤ x...
whose underlying order is directed
Directed set
In mathematics, a directed set is a nonempty set A together with a reflexive and transitive binary relation ≤ , with the additional property that every pair of elements has an upper bound: In other words, for any a and b in A there must exist a c in A with a ≤ c and b ≤...
, whose positive cone is a refinement monoid, and which is unperforated, the letter meaning that mx≥0 implies that x≥0, for any element x of G and any positive integer m. Any simplicial group, that is, a partially ordered abelian group of the form
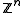, is a dimension group. Effros, Handelman, and Shen proved in 1980 that dimension groups are exactly the direct limitDirect limit
In mathematics, a direct limit is a colimit of a "directed family of objects". We will first give the definition for algebraic structures like groups and modules, and then the general definition which can be used in any category.- Algebraic objects :In this section objects are understood to be...
s of simplicial groups, where the transition maps are positive homomorphisms. This result had already been proved in 1976, in a slightly different form, by P.A. Grillet. Elliott proved in 1976 that the positive cone of any countable direct limit of simplicial groups is isomorphic to V(R), for some locally matricial ring R. Finally, Goodearl and Handelman proved in 1986 that the positive cone of any dimension group with at most ℵ1 elements is isomorphic to V(R), for some locally matricial ring R (over any given field).
Wehrung proved in 1998 that there are dimension groups with order-unit whose positive cone cannot be represented as V(R), for a von Neumann regular ring R. The given examples can have any cardinality greater than or equal to ℵ2. Whether any conical refinement monoid with at most ℵ1 (or even ℵ0) elements can be represented as V(R) for R von Neumann regular is an open problem.