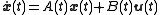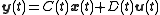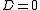Realization (systems)
Encyclopedia
Realization, in the system theory context refers to a state space
model implementing a given input-output behavior. That is, given an input-output relationship, a realization is a quadruple of (time-varying
) matrices
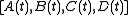such that
with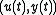
describing the input and output of the system at time 
.
,
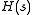, a realization is any quadruple of matrices 
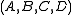such that 
.
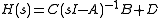can easily be transferred into state-space by the following approach (this example is for a 4-dimensional, single-input, single-output system)):
Given a transfer function, expand it to reveal all coefficients in both the numerator and denominator. This should result in the following form: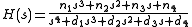
.
The coefficients can now be inserted directly into the state-space model by the following approach:
.
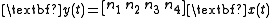This state-space realization is called controllable canonical form because the resulting model is guaranteed to be controllable
(i.e., because the control enters a chain of integrators, it has the ability to move every state).
The transfer function coefficients can also be used to construct another type of canonical form
.
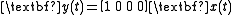This state-space realization is called observable canonical form because the resulting model is guaranteed to be observable
(i.e., because the output exits from a chain of integrators, every state has an effect on the output).
If we have an input 
, an output 
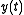, and a weighting pattern
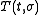then a realization is any triple of matrices 
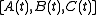such that 
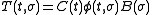where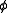 
is the state-transition matrix
associated with the realization.
) or can only include the output data (e.g. frequency domain decomposition). Typically an input-output technique would be more accurate, but the input data is not always available.
State space (controls)
In control engineering, a state space representation is a mathematical model of a physical system as a set of input, output and state variables related by first-order differential equations...
model implementing a given input-output behavior. That is, given an input-output relationship, a realization is a quadruple of (time-varying
Time-variant system
A time-variant system is a system that is not time invariant . Roughly speaking, characteristics of its output depend explicitly upon time.- Overview :...
) matrices
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
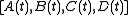such that
with
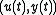describing the input and output of the system at time .LTI System
For a linear time-invariant system specified by a transfer matrixTransfer function
A transfer function is a mathematical representation, in terms of spatial or temporal frequency, of the relation between the input and output of a linear time-invariant system. With optical imaging devices, for example, it is the Fourier transform of the point spread function i.e...
,
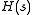, a realization is any quadruple of matrices 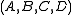such that 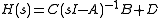.Canonical realizations
Any given transfer function which is strictly properStrictly proper
In control theory, a strictly proper transfer function is a transfer function where the degree of the numerator is less than the degree of the denominator.-Example:...
can easily be transferred into state-space by the following approach (this example is for a 4-dimensional, single-input, single-output system)):
Given a transfer function, expand it to reveal all coefficients in both the numerator and denominator. This should result in the following form:
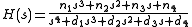.The coefficients can now be inserted directly into the state-space model by the following approach:
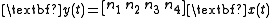.This state-space realization is called controllable canonical form because the resulting model is guaranteed to be controllable
Controllability
Controllability is an important property of a control system, and the controllability property plays a crucial role in many control problems, such as stabilization of unstable systems by feedback, or optimal control....
(i.e., because the control enters a chain of integrators, it has the ability to move every state).
The transfer function coefficients can also be used to construct another type of canonical form
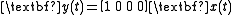.This state-space realization is called observable canonical form because the resulting model is guaranteed to be observable
Observability
Observability, in control theory, is a measure for how well internal states of a system can be inferred by knowledge of its external outputs. The observability and controllability of a system are mathematical duals. The concept of observability was introduced by American-Hungarian scientist Rudolf E...
(i.e., because the output exits from a chain of integrators, every state has an effect on the output).
, an output 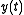, and a weighting patternWeighting pattern
A weighting pattern for a linear dynamical system describes the relationship between an input u and output y. Given the time-variant system described by...
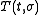then a realization is any triple of matrices 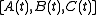such that 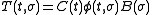where 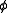is the state-transition matrixState-transition matrix
In control theory, the state-transition matrix is a matrix whose product with the state vector x at an initial time t_0 gives x at a later time t. The state-transition matrix can be used to obtain the general solution of linear dynamical systems...
associated with the realization.
System identification
System identification techniques take the experimental data from a system and output a realization. Such techniques can utilize both input and output data (e.g. eigensystem realization algorithmEigensystem realization algorithm
The Eigensystem realization algorithm is a system identification technique popular in civil engineering, in particular in structural health monitoring...
) or can only include the output data (e.g. frequency domain decomposition). Typically an input-output technique would be more accurate, but the input data is not always available.