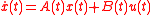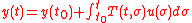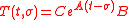Weighting pattern
Encyclopedia
A weighting pattern for a linear dynamical system
describes the relationship between an input and output
and output 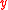 . Given the time-variant system
. Given the time-variant system
described by
then the output can be written as
where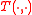 is the weighting pattern for the system. For such a system the weighting pattern is
is the weighting pattern for the system. For such a system the weighting pattern is 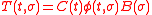 such that
such that  is the state transition matrix.
is the state transition matrix.
The weighting pattern will determine a system, but note that if there exists a realization
for this weighting pattern then there exists many that do so.
Continuous
where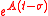 is the matrix exponential
is the matrix exponential
.
Discrete
Linear dynamical system
Linear dynamical systems are a special type of dynamical system where the equation governing the system's evolution is linear. While dynamical systems in general do not have closed-form solutions, linear dynamical systems can be solved exactly, and they have a rich set of mathematical properties...
describes the relationship between an input
 and output
and output 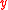 . Given the time-variant system
. Given the time-variant systemTime-variant system
A time-variant system is a system that is not time invariant . Roughly speaking, characteristics of its output depend explicitly upon time.- Overview :...
described by
then the output can be written as
where
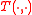 is the weighting pattern for the system. For such a system the weighting pattern is
is the weighting pattern for the system. For such a system the weighting pattern is 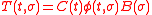 such that
such that  is the state transition matrix.
is the state transition matrix.The weighting pattern will determine a system, but note that if there exists a realization
Realization (systems)
Realization, in the system theory context refers to a state space model implementing a given input-output behavior. That is, given an input-output relationship, a realization is a quadruple of matrices [A,B,C,D] such that-LTI System:...
for this weighting pattern then there exists many that do so.
Linear time invariant system
In a LTI system then the weighting pattern is:Continuous
where
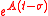 is the matrix exponential
is the matrix exponentialMatrix exponential
In mathematics, the matrix exponential is a matrix function on square matrices analogous to the ordinary exponential function. Abstractly, the matrix exponential gives the connection between a matrix Lie algebra and the corresponding Lie group....
.
Discrete
-
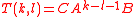 .
.