Reaction–diffusion system
Encyclopedia
Reaction–diffusion systems are mathematical models which explain how the concentration of one or more substances distributed in space changes under the influence of two processes: local chemical reaction
s in which the substances are transformed into each other, and diffusion
which causes the substances to spread out over a surface in space.
This description implies that reaction–diffusion systems are naturally applied in chemistry
. However, the system can also describe dynamical processes of non-chemical nature. Examples are found in biology
, geology
and physics
and ecology
. Mathematically, reaction–diffusion systems take the form of semi-linear parabolic partial differential equation
s. They can be represented in the general form
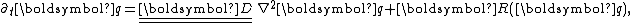
where each component of the vector q(x,t) represents the concentration of one substance, is a diagonal matrix
of diffusion coefficients, and R accounts for all local reactions. The solutions of reaction–diffusion equations display a wide range of behaviours, including the formation of travelling waves
and wave-like phenomena as well as other self-organized
patterns
like stripes, hexagons or more intricate structure like dissipative solitons.
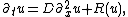
is also referred to as the KPP (Kolmogorov-Petrovsky-Piskounov) equation. If the reaction term vanishes, then the equation represents a pure diffusion process. The corresponding equation is Fick's second law. The choice R(u) = u(1-u) yields Fisher's equation
that was originally used to describe the spreading of biological population
s, the Newell-Whitehead-Segel equation with R(u) = u(1 − u2) to describe Rayleigh-Benard convection, the more general Zeldovich equation with R(u) = u(1 − u)(u − α) and 0 < α < 1 that arises in combustion
theory, and its particular degenerate case with R(u) = u2 − u3 that is sometimes referred to as the Zeldovich equation as well.
The dynamics of one-component systems is subject to certain restrictions as the evolution equation can also be written in the variational form
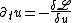
and therefore describes a permanent decrease of the "free energy"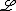 given by the functional
given by the functional
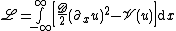
with a potential V(u) such that R(u)=dV(u)/du.
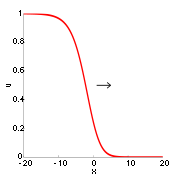 In systems with more than one stationary homogeneous solution, a typical solution is given by travelling fronts connecting the homogeneous states. These solutions move with constant speed without changing their shape and are of the form u(x, t) = û(ξ) with ξ = x − ct, where c is the speed of the travelling wave. Note that while travelling waves are generically stable structures, all non-monotonous stationary solutions (e.g. localized domains composed of a front-antifront pair) are unstable. For c = 0, there is a
In systems with more than one stationary homogeneous solution, a typical solution is given by travelling fronts connecting the homogeneous states. These solutions move with constant speed without changing their shape and are of the form u(x, t) = û(ξ) with ξ = x − ct, where c is the speed of the travelling wave. Note that while travelling waves are generically stable structures, all non-monotonous stationary solutions (e.g. localized domains composed of a front-antifront pair) are unstable. For c = 0, there is a
simple proof for this statement: if u0(x) is a stationary solution and u=u0(x) + ũ(x, t) is an infinitesimally perturbed solution, linear stability analysis yields the equation
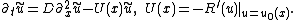
With the ansatz ũ = ψ(x)exp(−λt) we arrive at the eigenvalue problem
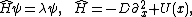
of Schrödinger type
where negative eigenvalues result in the instability of the solution. Due to translational invariance ψ = ∂xu0(x) is a neutral eigenfunction
with the eigenvalue λ = 0, and all other eigenfunctions can be sorted according to an increasing number of knots with the magnitude of the corresponding real eigenvalue increases monotonically with the number of zeros. The eigenfunction ψ = ∂x u0(x) should have at least one zero, and for a non-monotonic stationary solution the corresponding eigenvalue λ = 0 cannot be the
lowest one, thereby implying instability.
To determine the velocity c of a moving front, one may go to a moving coordinate system and look at stationary solutions:
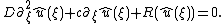
This equation has a nice mechanical analogue as the motion of a
mass D with position û in the course of the "time" ξ under
the force R with the damping coefficient c which allows for a
rather illustrative access to the construction of different
types of solutions and the determination of c.
When going from one to more space dimensions, a number of
statements from one-dimensional systems can still be applied.
Planar or curved wave fronts are typical structures, and a new
effect arises as the local velocity of a curved front becomes
dependent on the local radius of curvature
(this can be
seen by going to polar coordinates). This phenomenon leads
to the so-called curvature-driven instability.
phenomena than their one-component counterparts. An important
idea that was first proposed by Alan Turing
is that a state
that is stable in the local system should become unstable in
the presence of diffusion
. This idea seems
unintuitive at first glance as diffusion is commonly
associated with a stabilizing effect.
A linear stability analysis however shows that when linearizing
the general two-component system
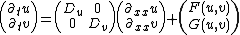
a plane wave
perturbation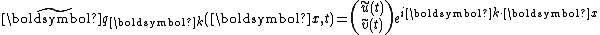
of the stationary homogeneous solution will satisfy
Turing's idea can only be realized in four
equivalence classes of systems characterized
by the signs of the Jacobian
R' of the reaction function. In particular, if a finite
wave vector k is supposed to be the most unstable one,
the Jacobian must have the signs
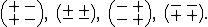
This class of systems is named activator-inhibitor system
after its first representative: close to the ground state, one
component stimulates the production of both components while
the other one inhibits their growth. Its most prominent
representative is the FitzHugh–Nagumo equation
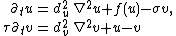
with ƒ(u) = λu − u3 − κ which describes how an action potential
travels
through a nerve. Here, du,
dv, τ, σ and λ are
positive constants.
When an activator-inhibitor system undergoes a change of parameters, one may pass
from conditions under which a homogeneous ground state is
stable to conditions under which it is linearly unstable. The
corresponding bifurcation
may be either
a Hopf bifurcation
to a globally oscillating homogeneous
state with a dominant wave number k = 0 or a
Turing bifurcation to a globally patterned state with
a dominant finite wave number. The latter in two
spatial dimensions typically leads to stripe or hexagonal
patterns.
For the Fitzhugh-Nagumo example, the neutral stability curves marking the
boundary of the linearly stable region for the Turing and Hopf
bifurcation are given by
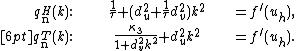
If the bifurcation is subcritical, often localized structures
(dissipative solitons) can be observed in the
hysteretic
region where the pattern coexists
with the ground state. Other frequently encountered structures
comprise pulse trains,
spiral waves and target patterns.
more than two components have been proposed, e.g. as models
for the Belousov-Zhabotinsky reaction
,
, for blood clotting or planar gas discharge systems.
While it is known that systems with more components allow for
a variety of phenomena not possible in systems with one or two
components (e.g. stable running pulses in more than one spatial
dimension without global feedback), up to now a systematic
overview of the possible phenomena in dependence on the properties
of the underlying system is hardly present.
. The above-mentioned patterns (fronts, spirals, targets, hexagons, stripes and dissipative solitons) can be found in various types of reaction-diffusion systems in spite of large discrepancies e.g. in the local reaction terms. It has also been argued that reaction-diffusion processes are an essential basis for processes connected to morphogenesis
in biology and may even be related to animal coats and skin pigmentation.
Another reason for the interest in reaction-diffusion systems is that although they represent nonlinear partial differential equation, there are often possibilities for an analytical treatment.
been realized in three ways. First, gel reactors or filled capillary tubes may be used. Second, temperature
pulses on catalytic surfaces
have been investigated.
Third, the propagation of running nerve pulses is modelled
using reaction-diffusion systems.
Aside from these generic examples, it has turned out that under appropriate
circumstances electric transport systems like plasmas or semiconductors can be
described in a reaction-diffusion approach. For these systems various experiments
on pattern formation have been carried out.
Chemical reaction
A chemical reaction is a process that leads to the transformation of one set of chemical substances to another. Chemical reactions can be either spontaneous, requiring no input of energy, or non-spontaneous, typically following the input of some type of energy, such as heat, light or electricity...
s in which the substances are transformed into each other, and diffusion
Diffusion
Molecular diffusion, often called simply diffusion, is the thermal motion of all particles at temperatures above absolute zero. The rate of this movement is a function of temperature, viscosity of the fluid and the size of the particles...
which causes the substances to spread out over a surface in space.
This description implies that reaction–diffusion systems are naturally applied in chemistry
Chemistry
Chemistry is the science of matter, especially its chemical reactions, but also its composition, structure and properties. Chemistry is concerned with atoms and their interactions with other atoms, and particularly with the properties of chemical bonds....
. However, the system can also describe dynamical processes of non-chemical nature. Examples are found in biology
Biology
Biology is a natural science concerned with the study of life and living organisms, including their structure, function, growth, origin, evolution, distribution, and taxonomy. Biology is a vast subject containing many subdivisions, topics, and disciplines...
, geology
Geology
Geology is the science comprising the study of solid Earth, the rocks of which it is composed, and the processes by which it evolves. Geology gives insight into the history of the Earth, as it provides the primary evidence for plate tectonics, the evolutionary history of life, and past climates...
and physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
and ecology
Ecology
Ecology is the scientific study of the relations that living organisms have with respect to each other and their natural environment. Variables of interest to ecologists include the composition, distribution, amount , number, and changing states of organisms within and among ecosystems...
. Mathematically, reaction–diffusion systems take the form of semi-linear parabolic partial differential equation
Parabolic partial differential equation
A parabolic partial differential equation is a type of second-order partial differential equation , describing a wide family of problems in science including heat diffusion, ocean acoustic propagation, in physical or mathematical systems with a time variable, and which behave essentially like heat...
s. They can be represented in the general form
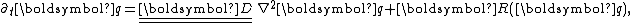
where each component of the vector q(x,t) represents the concentration of one substance, is a diagonal matrix
Diagonal matrix
In linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...
of diffusion coefficients, and R accounts for all local reactions. The solutions of reaction–diffusion equations display a wide range of behaviours, including the formation of travelling waves
and wave-like phenomena as well as other self-organized
Self-organization
Self-organization is the process where a structure or pattern appears in a system without a central authority or external element imposing it through planning...
patterns
Pattern formation
The science of pattern formation deals with the visible, orderly outcomes of self-organisation and the common principles behind similar patterns....
like stripes, hexagons or more intricate structure like dissipative solitons.
One-component reaction–diffusion equations
The most simple reaction–diffusion equation concerning the concentration u of a single substance in one spatial dimension,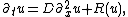
is also referred to as the KPP (Kolmogorov-Petrovsky-Piskounov) equation. If the reaction term vanishes, then the equation represents a pure diffusion process. The corresponding equation is Fick's second law. The choice R(u) = u(1-u) yields Fisher's equation
Fisher's equation
In mathematics, Fisher's equation, also known as the Fisher-Kolmogorov equation and the Fisher-KPP equation, named after R. A. Fisher and A. N...
that was originally used to describe the spreading of biological population
Population
A population is all the organisms that both belong to the same group or species and live in the same geographical area. The area that is used to define a sexual population is such that inter-breeding is possible between any pair within the area and more probable than cross-breeding with individuals...
s, the Newell-Whitehead-Segel equation with R(u) = u(1 − u2) to describe Rayleigh-Benard convection, the more general Zeldovich equation with R(u) = u(1 − u)(u − α) and 0 < α < 1 that arises in combustion
Combustion
Combustion or burning is the sequence of exothermic chemical reactions between a fuel and an oxidant accompanied by the production of heat and conversion of chemical species. The release of heat can result in the production of light in the form of either glowing or a flame...
theory, and its particular degenerate case with R(u) = u2 − u3 that is sometimes referred to as the Zeldovich equation as well.
The dynamics of one-component systems is subject to certain restrictions as the evolution equation can also be written in the variational form
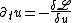
and therefore describes a permanent decrease of the "free energy"
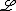 given by the functional
given by the functional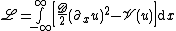
with a potential V(u) such that R(u)=dV(u)/du.

simple proof for this statement: if u0(x) is a stationary solution and u=u0(x) + ũ(x, t) is an infinitesimally perturbed solution, linear stability analysis yields the equation
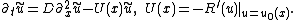
With the ansatz ũ = ψ(x)exp(−λt) we arrive at the eigenvalue problem
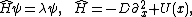
of Schrödinger type
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
where negative eigenvalues result in the instability of the solution. Due to translational invariance ψ = ∂xu0(x) is a neutral eigenfunction
Eigenfunction
In mathematics, an eigenfunction of a linear operator, A, defined on some function space is any non-zero function f in that space that returns from the operator exactly as is, except for a multiplicative scaling factor. More precisely, one has...
with the eigenvalue λ = 0, and all other eigenfunctions can be sorted according to an increasing number of knots with the magnitude of the corresponding real eigenvalue increases monotonically with the number of zeros. The eigenfunction ψ = ∂x u0(x) should have at least one zero, and for a non-monotonic stationary solution the corresponding eigenvalue λ = 0 cannot be the
lowest one, thereby implying instability.
To determine the velocity c of a moving front, one may go to a moving coordinate system and look at stationary solutions:
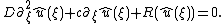
This equation has a nice mechanical analogue as the motion of a
mass D with position û in the course of the "time" ξ under
the force R with the damping coefficient c which allows for a
rather illustrative access to the construction of different
types of solutions and the determination of c.
When going from one to more space dimensions, a number of
statements from one-dimensional systems can still be applied.
Planar or curved wave fronts are typical structures, and a new
effect arises as the local velocity of a curved front becomes
dependent on the local radius of curvature
Curvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
(this can be
seen by going to polar coordinates). This phenomenon leads
to the so-called curvature-driven instability.
Two-component reaction–diffusion equations
Two-component systems allow for a much larger range of possiblephenomena than their one-component counterparts. An important
idea that was first proposed by Alan Turing
Alan Turing
Alan Mathison Turing, OBE, FRS , was an English mathematician, logician, cryptanalyst, and computer scientist. He was highly influential in the development of computer science, providing a formalisation of the concepts of "algorithm" and "computation" with the Turing machine, which played a...
is that a state
that is stable in the local system should become unstable in
the presence of diffusion
Diffusion
Molecular diffusion, often called simply diffusion, is the thermal motion of all particles at temperatures above absolute zero. The rate of this movement is a function of temperature, viscosity of the fluid and the size of the particles...
. This idea seems
unintuitive at first glance as diffusion is commonly
associated with a stabilizing effect.
A linear stability analysis however shows that when linearizing
the general two-component system
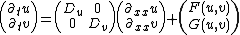
a plane wave
Plane wave
In the physics of wave propagation, a plane wave is a constant-frequency wave whose wavefronts are infinite parallel planes of constant peak-to-peak amplitude normal to the phase velocity vector....
perturbation
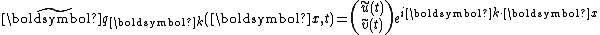
of the stationary homogeneous solution will satisfy

Turing's idea can only be realized in four
equivalence classes of systems characterized
by the signs of the Jacobian
Jacobian
In vector calculus, the Jacobian matrix is the matrix of all first-order partial derivatives of a vector- or scalar-valued function with respect to another vector. Suppose F : Rn → Rm is a function from Euclidean n-space to Euclidean m-space...
R' of the reaction function. In particular, if a finite
wave vector k is supposed to be the most unstable one,
the Jacobian must have the signs
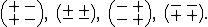
This class of systems is named activator-inhibitor system
after its first representative: close to the ground state, one
component stimulates the production of both components while
the other one inhibits their growth. Its most prominent
representative is the FitzHugh–Nagumo equation
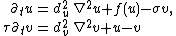
with ƒ(u) = λu − u3 − κ which describes how an action potential
Action potential
In physiology, an action potential is a short-lasting event in which the electrical membrane potential of a cell rapidly rises and falls, following a consistent trajectory. Action potentials occur in several types of animal cells, called excitable cells, which include neurons, muscle cells, and...
travels
through a nerve. Here, du,
dv, τ, σ and λ are
positive constants.
When an activator-inhibitor system undergoes a change of parameters, one may pass
from conditions under which a homogeneous ground state is
stable to conditions under which it is linearly unstable. The
corresponding bifurcation
Bifurcation theory
Bifurcation theory is the mathematical study of changes in the qualitative or topological structure of a given family, such as the integral curves of a family of vector fields, and the solutions of a family of differential equations...
may be either
a Hopf bifurcation
Hopf bifurcation
In the mathematical theory of bifurcations, a Hopf or Poincaré–Andronov–Hopf bifurcation, named after Henri Poincaré, Eberhard Hopf, and Aleksandr Andronov, is a local bifurcation in which a fixed point of a dynamical system loses stability as a pair of complex conjugate eigenvalues of...
to a globally oscillating homogeneous
state with a dominant wave number k = 0 or a
Turing bifurcation to a globally patterned state with
a dominant finite wave number. The latter in two
spatial dimensions typically leads to stripe or hexagonal
patterns.
For the Fitzhugh-Nagumo example, the neutral stability curves marking the
boundary of the linearly stable region for the Turing and Hopf
bifurcation are given by
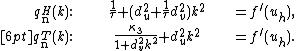
If the bifurcation is subcritical, often localized structures
(dissipative solitons) can be observed in the
hysteretic
Hysteresis
Hysteresis is the dependence of a system not just on its current environment but also on its past. This dependence arises because the system can be in more than one internal state. To predict its future evolution, either its internal state or its history must be known. If a given input alternately...
region where the pattern coexists
with the ground state. Other frequently encountered structures
comprise pulse trains,
spiral waves and target patterns.
Three- and more-component reaction–diffusion equations
For a variety of systems, reaction-diffusion equations withmore than two components have been proposed, e.g. as models
for the Belousov-Zhabotinsky reaction
Belousov-Zhabotinsky reaction
A Belousov–Zhabotinsky reaction, or BZ reaction, is one of a class of reactions that serve as a classical example of non-equilibrium thermodynamics, resulting in the establishment of a nonlinear chemical oscillator. The only common element in these oscillating systems is the inclusion of bromine...
,
, for blood clotting or planar gas discharge systems.
While it is known that systems with more components allow for
a variety of phenomena not possible in systems with one or two
components (e.g. stable running pulses in more than one spatial
dimension without global feedback), up to now a systematic
overview of the possible phenomena in dependence on the properties
of the underlying system is hardly present.
Applications and universality
In recent times, reaction–diffusion systems have attracted much interest as a prototype model for pattern formationPattern formation
The science of pattern formation deals with the visible, orderly outcomes of self-organisation and the common principles behind similar patterns....
. The above-mentioned patterns (fronts, spirals, targets, hexagons, stripes and dissipative solitons) can be found in various types of reaction-diffusion systems in spite of large discrepancies e.g. in the local reaction terms. It has also been argued that reaction-diffusion processes are an essential basis for processes connected to morphogenesis
Morphogenesis
Morphogenesis , is the biological process that causes an organism to develop its shape...
in biology and may even be related to animal coats and skin pigmentation.
Another reason for the interest in reaction-diffusion systems is that although they represent nonlinear partial differential equation, there are often possibilities for an analytical treatment.
Experiments
Well-controllable experiments in chemical reaction-diffusion systems have up to nowbeen realized in three ways. First, gel reactors or filled capillary tubes may be used. Second, temperature
Temperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
pulses on catalytic surfaces
Catalytic converter
A catalytic converter is a device used to convert toxic exhaust emissions from an internal combustion engine into non-toxic substances. Inside a catalytic converter, a catalyst stimulates a chemical reaction in which noxious byproducts of combustion are converted to less toxic substances by dint...
have been investigated.
Third, the propagation of running nerve pulses is modelled
using reaction-diffusion systems.
Aside from these generic examples, it has turned out that under appropriate
circumstances electric transport systems like plasmas or semiconductors can be
described in a reaction-diffusion approach. For these systems various experiments
on pattern formation have been carried out.
See also
- Diffusion-controlled reaction
- Chemical kineticsChemical kineticsChemical kinetics, also known as reaction kinetics, is the study of rates of chemical processes. Chemical kinetics includes investigations of how different experimental conditions can influence the speed of a chemical reaction and yield information about the reaction's mechanism and transition...
- Phase space methodPhase space methodIn applied mathematics, the phase space method is a technique for constructing and analyzing solutions of dynamical systems, that is, solving time-dependent differential equations. The method consists of first rewriting the equations as a system of differential equations that are first-order in...
- Fisher's equationFisher's equationIn mathematics, Fisher's equation, also known as the Fisher-Kolmogorov equation and the Fisher-KPP equation, named after R. A. Fisher and A. N...
- Autocatalytic reactions and order creation
- Pattern formationPattern formationThe science of pattern formation deals with the visible, orderly outcomes of self-organisation and the common principles behind similar patterns....
- Stochastic geometryStochastic geometryIn mathematics, stochastic geometry is the study of random spatial patterns. At the heart of the subject lies the study of random point patterns...
- MCloneMCloneMClone, or Clonal Mosaic, is a pattern formation algorithm proposed in 1998 used specially for simulating giraffes and members of the Phelidae family of the mammalians. It was primarily proposed as a 2D model and lately was extended to 3D...
External links
- Java applet showing a reaction–diffusion simulation
- Another applet showing Gray-Scott reaction-diffusion.
- Gallery of reaction-diffusion images and movies.
- TexRD software random texture generator based on reaction-diffusion for graphists and scientific use
- Reaction-Diffusion by the Gray-Scott Model: Pearson's parameterization a visual map of the parameter space of Gray-Scott reaction diffusion.
- A Thesis on reaction-diffusion patterns with an overview of the field

