
Random measure
Encyclopedia
In probability theory
, a random measure is a measure
-valued random element
. A random measure of the form
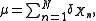
where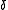 is the Dirac measure, and
is the Dirac measure, and 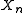 are random variables, is called a point process
are random variables, is called a point process
or random counting measure. This random measure describes the set of N particles, whose locations are given by the (generally vector valued) random variables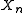 . The definitions of expectation measure, Laplace functional, moment measures and stationarity for random measures follow those of point process
. The definitions of expectation measure, Laplace functional, moment measures and stationarity for random measures follow those of point process
es. Random measures are useful in the description and analysis of Monte Carlo method
s, such as Monte Carlo numerical quadrature and particle filter
s.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, a random measure is a measure
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
-valued random element
Random element
In probability theory, random element is a generalization of the concept of random variable to more complicated spaces than the simple real line...
. A random measure of the form
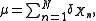
where
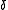 is the Dirac measure, and
is the Dirac measure, and 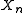 are random variables, is called a point process
are random variables, is called a point processPoint process
In statistics and probability theory, a point process is a type of random process for which any one realisation consists of a set of isolated points either in time or geographical space, or in even more general spaces...
or random counting measure. This random measure describes the set of N particles, whose locations are given by the (generally vector valued) random variables
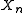 . The definitions of expectation measure, Laplace functional, moment measures and stationarity for random measures follow those of point process
. The definitions of expectation measure, Laplace functional, moment measures and stationarity for random measures follow those of point processPoint process
In statistics and probability theory, a point process is a type of random process for which any one realisation consists of a set of isolated points either in time or geographical space, or in even more general spaces...
es. Random measures are useful in the description and analysis of Monte Carlo method
Monte Carlo method
Monte Carlo methods are a class of computational algorithms that rely on repeated random sampling to compute their results. Monte Carlo methods are often used in computer simulations of physical and mathematical systems...
s, such as Monte Carlo numerical quadrature and particle filter
Particle filter
In statistics, particle filters, also known as Sequential Monte Carlo methods , are sophisticated model estimation techniques based on simulation...
s.
See also
- Point processPoint processIn statistics and probability theory, a point process is a type of random process for which any one realisation consists of a set of isolated points either in time or geographical space, or in even more general spaces...
- Poisson random measure
- Random elementRandom elementIn probability theory, random element is a generalization of the concept of random variable to more complicated spaces than the simple real line...
- Vector measureVector measureIn mathematics, a vector measure is a function defined on a family of sets and taking vector values satisfying certain properties. It is a generalization of the concept of measure, which takes nonnegative real values only.-Definitions and first consequences:...
- Ensemble

