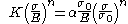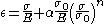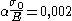
Ramberg-Osgood relationship
Encyclopedia
The Ramberg–Osgood equation was created to describe the non linear relationship between stress
and strain
—that is, the stress–strain curve—in materials near their yield points
. It is especially useful for metals that harden with plastic deformation (see strain hardening
), showing a smooth elastic-plastic transition.
In its original form, the equation for strain (deformation) is
where
The first term on the right side,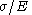
, is equal to the elastic part of the strain, while the second term, 
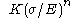, accounts for the plastic part, the parameters 
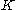and 
describing the hardening behavior of the material. Introducing the yield strength of the material, 
, and defining a new parameter, 
, related to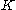 
as 
, it is convenient to rewrite the term on the extreme right side as follows:
Replacing in the first expression, the Ramberg–Osgood equation can be written as
and 
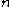. Due to the power-law
relationship between stress and plastic strain, the Ramberg–Osgood model implies that plastic strain is present even for very low levels of stress. Nevertheless, for low applied stresses and for the commonly used values of the material constants
and 
, the plastic strain remains negligible compared to the elastic strain. On the other hand, for stress levels higher than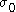 
, plastic strain becomes progressively larger than elastic strain.
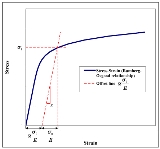
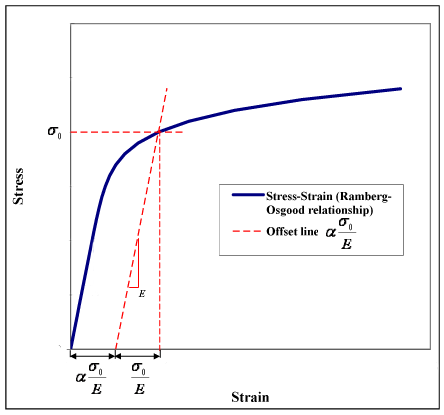
The value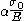
can be seen as a yield offset, as shown in figure 1. This comes from the fact that 
, when 
.
Accordingly (see Figure 1):
Commonly used values for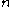
are ~5 or greater, although more precise values are usually obtained by fitting of tensile (or compressive) experimental data. Values for 
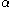can also be found by means of fitting to experimental data, although for some materials, it can be fixed in order to have the yield offset equal to the accepted value of strain of 0.2%, which means:
Stress (physics)
In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
and strain
Strain (materials science)
In continuum mechanics, the infinitesimal strain theory, sometimes called small deformation theory, small displacement theory, or small displacement-gradient theory, deals with infinitesimal deformations of a continuum body...
—that is, the stress–strain curve—in materials near their yield points
Yield (engineering)
The yield strength or yield point of a material is defined in engineering and materials science as the stress at which a material begins to deform plastically. Prior to the yield point the material will deform elastically and will return to its original shape when the applied stress is removed...
. It is especially useful for metals that harden with plastic deformation (see strain hardening
Work hardening
Work hardening, also known as strain hardening or cold working, is the strengthening of a metal by plastic deformation. This strengthening occurs because of dislocation movements within the crystal structure of the material. Any material with a reasonably high melting point such as metals and...
), showing a smooth elastic-plastic transition.
In its original form, the equation for strain (deformation) is
where
-
is strainStrain (materials science)In continuum mechanics, the infinitesimal strain theory, sometimes called small deformation theory, small displacement theory, or small displacement-gradient theory, deals with infinitesimal deformations of a continuum body...
, -
is stressStress (physics)In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
, -
is Young's modulusYoung's modulusYoung's modulus is a measure of the stiffness of an elastic material and is a quantity used to characterize materials. It is defined as the ratio of the uniaxial stress over the uniaxial strain in the range of stress in which Hooke's Law holds. In solid mechanics, the slope of the stress-strain...
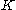, and -
and 
are constants that depend on the material being considered.
The first term on the right side,
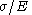, is equal to the elastic part of the strain, while the second term, 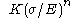, accounts for the plastic part, the parameters 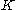and describing the hardening behavior of the material. Introducing the yield strength of the material, 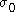, and defining a new parameter, , related to 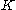as , it is convenient to rewrite the term on the extreme right side as follows:
Replacing in the first expression, the Ramberg–Osgood equation can be written as
Hardening behavior and yield offset
In the last form of the Ramberg–Osgood model, the hardening behavior of the material depends on the material constants and 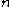. Due to the power-lawPower law
A power law is a special kind of mathematical relationship between two quantities. When the frequency of an event varies as a power of some attribute of that event , the frequency is said to follow a power law. For instance, the number of cities having a certain population size is found to vary...
relationship between stress and plastic strain, the Ramberg–Osgood model implies that plastic strain is present even for very low levels of stress. Nevertheless, for low applied stresses and for the commonly used values of the material constants
and , the plastic strain remains negligible compared to the elastic strain. On the other hand, for stress levels higher than 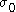, plastic strain becomes progressively larger than elastic strain.The value
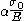can be seen as a yield offset, as shown in figure 1. This comes from the fact that , when .Accordingly (see Figure 1):
- elastic strain at yield =
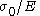
- plastic strain at yield =
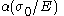= yield offset
Commonly used values for
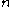are ~5 or greater, although more precise values are usually obtained by fitting of tensile (or compressive) experimental data. Values for 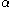can also be found by means of fitting to experimental data, although for some materials, it can be fixed in order to have the yield offset equal to the accepted value of strain of 0.2%, which means: