Quotient category
Encyclopedia
In mathematics
, a quotient category is a category
obtained from another one by identifying sets of morphism
s. The notion is similar to that of a quotient group
or quotient space
, but in the categorical setting.
R on C is given by: for each pair of objects X, Y in C, an equivalence relation
RX,Y on Hom(X,Y), such that the equivalence relations respect composition of morphisms. That is, if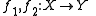
are related in Hom(X, Y) and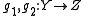
are related in Hom(Y, Z) then g1f1 and g2f2 are related in Hom(X, Z).
Given a congruence relation R on C we can define the quotient category C/R as the category whose objects are those of C and whose morphisms are equivalence classes of morphisms in C. That is,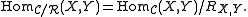
Composition of morphisms in C/R is well-defined
since R is a congruence relation.
There is also a notion of taking the quotient of an Abelian category
A by a Serre subcategory B. This is done as follows. The objects of A/B are the objects of A. Given two objects X and Y of A, we define the set of morphisms from X to Y in A/B to be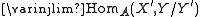
where the limit is over subobjects 
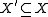and 
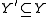such that 
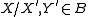. Then A/B is an Abelian category, and there is a canonical functor 
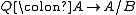. This Abelian quotient satisfies the universal property that if C is any other Abelian category, and 
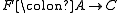is an exact functor
such that F(b) is a zero object of C for each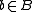
, then there is a unique exact functor 
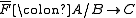such that 
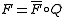. (See [Gabriel].)
from C to C/R which sends each morphism to its equivalence class. This functor is bijective on objects and surjective on Hom-sets (i.e. it is a full functor).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a quotient category is a category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
obtained from another one by identifying sets of morphism
Morphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
s. The notion is similar to that of a quotient group
Quotient group
In mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
or quotient space
Quotient space
In topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...
, but in the categorical setting.
Definition
Let C be a category. A congruence relationCongruence relation
In abstract algebra, a congruence relation is an equivalence relation on an algebraic structure that is compatible with the structure...
R on C is given by: for each pair of objects X, Y in C, an equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
RX,Y on Hom(X,Y), such that the equivalence relations respect composition of morphisms. That is, if
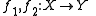
are related in Hom(X, Y) and
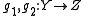
are related in Hom(Y, Z) then g1f1 and g2f2 are related in Hom(X, Z).
Given a congruence relation R on C we can define the quotient category C/R as the category whose objects are those of C and whose morphisms are equivalence classes of morphisms in C. That is,
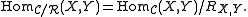
Composition of morphisms in C/R is well-defined
Well-defined
In mathematics, well-definition is a mathematical or logical definition of a certain concept or object which uses a set of base axioms in an entirely unambiguous way and satisfies the properties it is required to satisfy. Usually definitions are stated unambiguously, and it is clear they satisfy...
since R is a congruence relation.
There is also a notion of taking the quotient of an Abelian category
Abelian category
In mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototype example of an abelian category is the category of abelian groups, Ab. The theory originated in a tentative...
A by a Serre subcategory B. This is done as follows. The objects of A/B are the objects of A. Given two objects X and Y of A, we define the set of morphisms from X to Y in A/B to be
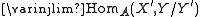where the limit is over subobjects 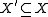and 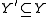such that 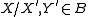. Then A/B is an Abelian category, and there is a canonical functor 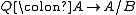. This Abelian quotient satisfies the universal property that if C is any other Abelian category, and 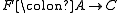is an exact functorExact functor
In homological algebra, an exact functor is a functor, from some category to another, which preserves exact sequences. Exact functors are very convenient in algebraic calculations, roughly speaking because they can be applied to presentations of objects easily...
such that F(b) is a zero object of C for each
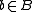, then there is a unique exact functor 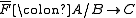such that 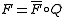. (See [Gabriel].)Properties
There is a natural quotient functorFunctor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
from C to C/R which sends each morphism to its equivalence class. This functor is bijective on objects and surjective on Hom-sets (i.e. it is a full functor).
Examples
- MonoidMonoidIn abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
s and groupGroup (mathematics)In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
may be regarded as categories with one object. In this case the quotient category coincides with the notion of a quotient monoid or a quotient groupQuotient groupIn mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
. - The homotopy category of topological spacesHomotopy category of topological spacesIn mathematics, a homotopy category is a category whose objects are topological spaces and whose morphisms are homotopy classes of continuous functions. The homotopy category of all topological spaces is often denoted hTop or Toph....
hTop is a quotient category of Top, the category of topological spacesCategory of topological spacesIn mathematics, the category of topological spaces, often denoted Top, is the category whose objects are topological spaces and whose morphisms are continuous maps. This is a category because the composition of two continuous maps is again continuous...
. The equivalence classes of morphisms are homotopy classes of continuous maps.