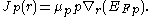Quasi Fermi level
Encyclopedia
A Quasi Fermi level is a term used in quantum mechanics
and especially in solid state physics for the new Fermi level
that describes the population of each type of charge carrier
(electron
s and holes
) in a semiconductor
separately when their populations are displaced from equilibrium
. This displacement could be caused by the application of an external electric potential
, which injects electrons and holes
, or by exposure to light
of energy
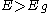, which increases the density
of both electrons and holes above their equilibrium values. The displacement from equilibrium is such that the carrier populations can no longer be described by a single Fermi level, and separate quasi-Fermi levels must be used for each charge carrier.
(In this article the term "Fermi level" is used to mean the same thing as chemical potential
. This is the most common usage in semiconductor physics, although in other areas of solid-state physics the term "Fermi level" means something different
, namely the chemical potential at zero temperature.)
When a semiconductor is in thermal equilibrium
, the distribution function of the electrons at the energy level of E is presented by Fermi-Dirac distribution function. In this case the Fermi level is defined as the level in which the probability of occupation of electron at that energy is 1/2. In thermal equilibrium, the electron quasi-Fermi level, hole quasi-Fermi level and Fermi level are equal.
When a disturbance from a thermal equilibrium situation occurs, the populations of holes
and electrons change. If the disturbance is not too great or not changing too quickly, the populations of electrons and holes each relax to a state of quasi thermal equilibrium. Because the relaxation time
for electrons within the conduction band
is much lower than across the band gap
, we can consider that the electrons are in thermal equilibrium in the conduction band. This is also applicable for holes in the valence band
. In the case of electrons we can define a quasi Fermi level and temperature due to thermal equilibrium of electrons in conduction band and quasi Fermi level for holes similarly.
We can state the general Fermi function for electrons in conduction band as
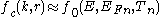
and for holes in valence band as
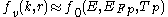
where:
This simplification will help us in many areas. For example, we can use the same equation for electron and hole densities used in thermal equilibrium, but substituting the Fermi levels and temperature. i.e.:
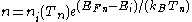
and
where
A current (due to the combined effects of drift
and diffusion
) will only flow if there is a variation in the Fermi or quasi Fermi level. The current density for electron flow can be shown to be proportional to the gradient in the electron quasi Fermi level as such:
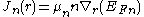, where 
is the electron mobility
, and
is the gradient
with respect to distance r.
Similarly, for holes, we have
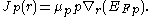
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
and especially in solid state physics for the new Fermi level
Fermi level
The Fermi level is a hypothetical level of potential energy for an electron inside a crystalline solid. Occupying such a level would give an electron a potential energy \epsilon equal to its chemical potential \mu as they both appear in the Fermi-Dirac distribution function,which...
that describes the population of each type of charge carrier
Charge carrier
In physics, a charge carrier is a free particle carrying an electric charge, especially the particles that carry electric currents in electrical conductors. Examples are electrons and ions...
(electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
s and holes
Electron hole
An electron hole is the conceptual and mathematical opposite of an electron, useful in the study of physics, chemistry, and electrical engineering. The concept describes the lack of an electron at a position where one could exist in an atom or atomic lattice...
) in a semiconductor
Semiconductor
A semiconductor is a material with electrical conductivity due to electron flow intermediate in magnitude between that of a conductor and an insulator. This means a conductivity roughly in the range of 103 to 10−8 siemens per centimeter...
separately when their populations are displaced from equilibrium
Thermodynamic equilibrium
In thermodynamics, a thermodynamic system is said to be in thermodynamic equilibrium when it is in thermal equilibrium, mechanical equilibrium, radiative equilibrium, and chemical equilibrium. The word equilibrium means a state of balance...
. This displacement could be caused by the application of an external electric potential
Electric potential
In classical electromagnetism, the electric potential at a point within a defined space is equal to the electric potential energy at that location divided by the charge there...
, which injects electrons and holes
Electron hole
An electron hole is the conceptual and mathematical opposite of an electron, useful in the study of physics, chemistry, and electrical engineering. The concept describes the lack of an electron at a position where one could exist in an atom or atomic lattice...
, or by exposure to light
Light
Light or visible light is electromagnetic radiation that is visible to the human eye, and is responsible for the sense of sight. Visible light has wavelength in a range from about 380 nanometres to about 740 nm, with a frequency range of about 405 THz to 790 THz...
of energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
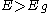, which increases the densityDensity
The mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...
of both electrons and holes above their equilibrium values. The displacement from equilibrium is such that the carrier populations can no longer be described by a single Fermi level, and separate quasi-Fermi levels must be used for each charge carrier.
(In this article the term "Fermi level" is used to mean the same thing as chemical potential
Chemical potential
Chemical potential, symbolized by μ, is a measure first described by the American engineer, chemist and mathematical physicist Josiah Willard Gibbs. It is the potential that a substance has to produce in order to alter a system...
. This is the most common usage in semiconductor physics, although in other areas of solid-state physics the term "Fermi level" means something different
Fermi level
The Fermi level is a hypothetical level of potential energy for an electron inside a crystalline solid. Occupying such a level would give an electron a potential energy \epsilon equal to its chemical potential \mu as they both appear in the Fermi-Dirac distribution function,which...
, namely the chemical potential at zero temperature.)
When a semiconductor is in thermal equilibrium
Thermal equilibrium
Thermal equilibrium is a theoretical physical concept, used especially in theoretical texts, that means that all temperatures of interest are unchanging in time and uniform in space...
, the distribution function of the electrons at the energy level of E is presented by Fermi-Dirac distribution function. In this case the Fermi level is defined as the level in which the probability of occupation of electron at that energy is 1/2. In thermal equilibrium, the electron quasi-Fermi level, hole quasi-Fermi level and Fermi level are equal.
When a disturbance from a thermal equilibrium situation occurs, the populations of holes
Electron hole
An electron hole is the conceptual and mathematical opposite of an electron, useful in the study of physics, chemistry, and electrical engineering. The concept describes the lack of an electron at a position where one could exist in an atom or atomic lattice...
and electrons change. If the disturbance is not too great or not changing too quickly, the populations of electrons and holes each relax to a state of quasi thermal equilibrium. Because the relaxation time
Relaxation time
In the physical sciences, relaxation usually means the return of a perturbed system into equilibrium.Each relaxation process can be characterized by a relaxation time τ...
for electrons within the conduction band
Conduction band
In the solid-state physics field of semiconductors and insulators, the conduction band is the range of electron energies, higher than that of the valence band, sufficient to free an electron from binding with its individual atom and allow it to move freely within the atomic lattice of the material...
is much lower than across the band gap
Band gap
In solid state physics, a band gap, also called an energy gap or bandgap, is an energy range in a solid where no electron states can exist. In graphs of the electronic band structure of solids, the band gap generally refers to the energy difference between the top of the valence band and the...
, we can consider that the electrons are in thermal equilibrium in the conduction band. This is also applicable for holes in the valence band
Valence band
In solids, the valence band is the highest range of electron energies in which electrons are normally present at absolute zero temperature....
. In the case of electrons we can define a quasi Fermi level and temperature due to thermal equilibrium of electrons in conduction band and quasi Fermi level for holes similarly.
We can state the general Fermi function for electrons in conduction band as
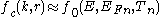
and for holes in valence band as
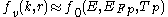
where:
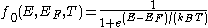is the Fermi-Dirac distribution function,
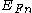is the electron quasi-fermi level at location r,
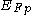is the hole quasi-fermi level at location r,
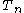is the electron temperature,
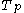is the hole temperature,
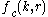is the probability that a particular conduction-band state, with wavevectorBloch's theorem* For the theorem named after Felix Bloch on wave functions of a particle in a periodic potential, see Bloch wave.* For the theorem in complex variables named after André Bloch, see Bloch's theorem ....
k and position r, is occupied by an electron,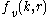
is the probability that a particular valence-band state, with wavevectorBloch's theorem* For the theorem named after Felix Bloch on wave functions of a particle in a periodic potential, see Bloch wave.* For the theorem in complex variables named after André Bloch, see Bloch's theorem ....
k and position r, is occupied by an electron, i.e. not occupied by a hole,
is the energy of the conduction- or valence-band state in question,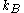
is Boltzmann's constant.
This simplification will help us in many areas. For example, we can use the same equation for electron and hole densities used in thermal equilibrium, but substituting the Fermi levels and temperature. i.e.:
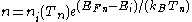
and
where
is the density (number per unit volume) of conduction electrons,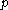
is the density of holes,
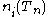is the density of conduction electrons that would be present in thermal equilibrium if the Fermi level were at 
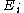and the temperature were 
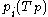is the density of holes that would be present in thermal equilibrium if the Fermi level were at 
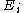and the temperature were 
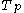,- This equation is valid in the Boltzmann approximationBoltzmann distributionIn chemistry, physics, and mathematics, the Boltzmann distribution is a certain distribution function or probability measure for the distribution of the states of a system. It underpins the concept of the canonical ensemble, providing its underlying distribution...
, i.e. assuming the electron and hole densities are not too high.
A current (due to the combined effects of drift
Drift velocity
The drift velocity is the average velocity that a particle, such as an electron, attains due to an electric field. It can also be referred to as Axial Drift Velocity since particles defined are assumed to be moving along a plane. In general, an electron will 'rattle around' in a conductor at the...
and diffusion
Diffusion
Molecular diffusion, often called simply diffusion, is the thermal motion of all particles at temperatures above absolute zero. The rate of this movement is a function of temperature, viscosity of the fluid and the size of the particles...
) will only flow if there is a variation in the Fermi or quasi Fermi level. The current density for electron flow can be shown to be proportional to the gradient in the electron quasi Fermi level as such:
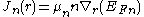, where is the electron mobilityElectron mobility
In solid-state physics, the electron mobility characterizes how quickly an electron can move through a metal or semiconductor, when pulled by an electric field. In semiconductors, there is an analogous quantity for holes, called hole mobility...
, and
is the gradientGradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
with respect to distance r.
Similarly, for holes, we have