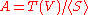Quadratic algebra
Encyclopedia
In mathematics
, a quadratic algebra is a filtered algebra
generated by degree one elements, with defining relations of degree 2. It was pointed out by Yuri Manin that such algebras play an important role in the theory of quantum group
s. The most important class of graded quadratic algebras is Koszul algebra
s.
of generators V = A1 and a subspace of homogeneous quadratic relations S ⊂ V ⊗ V . Thus
and inherits its grading from the tensor algebra
T(V). If the subspace of relations may also contain inhomogeneous degree 2 elements, S ⊂ k ⊕ V ⊕ (V ⊗ V), this construction results in a filtered quadratic algebra.
A graded quadratic algebra A as above admits a quadratic dual: the quadratic algebra generated by V* and with quadratic relations forming the orthogonal complement of S in V* ⊗ V*.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a quadratic algebra is a filtered algebra
Filtered algebra
In mathematics, a filtered algebra is a generalization of the notion of a graded algebra. Examples appear in many branches of mathematics, especially in homological algebra and representation theory....
generated by degree one elements, with defining relations of degree 2. It was pointed out by Yuri Manin that such algebras play an important role in the theory of quantum group
Quantum group
In mathematics and theoretical physics, the term quantum group denotes various kinds of noncommutative algebra with additional structure. In general, a quantum group is some kind of Hopf algebra...
s. The most important class of graded quadratic algebras is Koszul algebra
Koszul algebra
In abstract algebra, a Koszul algebra R is a graded k-algebra over which the residue field k has a linear minimal graded free resolution, i.e., there exists an exact sequence:...
s.
Definition
A graded quadratic algebra A is determined by a vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
of generators V = A1 and a subspace of homogeneous quadratic relations S ⊂ V ⊗ V . Thus
and inherits its grading from the tensor algebra
Tensor algebra
In mathematics, the tensor algebra of a vector space V, denoted T or T•, is the algebra of tensors on V with multiplication being the tensor product...
T(V). If the subspace of relations may also contain inhomogeneous degree 2 elements, S ⊂ k ⊕ V ⊕ (V ⊗ V), this construction results in a filtered quadratic algebra.
A graded quadratic algebra A as above admits a quadratic dual: the quadratic algebra generated by V* and with quadratic relations forming the orthogonal complement of S in V* ⊗ V*.
Examples
- Tensor algebraTensor algebraIn mathematics, the tensor algebra of a vector space V, denoted T or T•, is the algebra of tensors on V with multiplication being the tensor product...
, symmetric algebraSymmetric algebraIn mathematics, the symmetric algebra S on a vector space V over a field K is the free commutative unital associative algebra over K containing V....
and exterior algebraExterior algebraIn mathematics, the exterior product or wedge product of vectors is an algebraic construction used in Euclidean geometry to study areas, volumes, and their higher-dimensional analogs...
of a finite-dimensional vector spaceVector spaceA vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
are graded quadratic (in fact, Koszul) algebras.
- Universal enveloping algebraUniversal enveloping algebraIn mathematics, for any Lie algebra L one can construct its universal enveloping algebra U. This construction passes from the non-associative structure L to a unital associative algebra which captures the important properties of L.Any associative algebra A over the field K becomes a Lie algebra...
of a finite-dimensional Lie algebraLie algebraIn mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
is a filtered quadratic algebra.