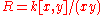Koszul algebra
Encyclopedia
In abstract algebra
, a Koszul algebra is a graded
is a graded
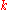 -algebra
-algebra
over which the residue field
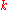 has a linear minimal graded free resolution, i.e., there exists an exact sequence
has a linear minimal graded free resolution, i.e., there exists an exact sequence
:
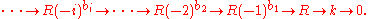
It is named after the French mathematician Jean-Louis Koszul
.
We can choose bases for the free modules in the resolution; then the maps can be written as matrices. For a Koszul algebra, the entries in the matrices are zero or linear forms.
An example of a Koszul algebra is a polynomial ring
over a field, for which the Koszul complex
is the minimal graded free resolution of the residue field. There are Koszul algebras whose residue fields have infinite minimal graded free resolutions, e.g,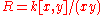
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, a Koszul algebra
 is a graded
is a gradedGraded algebra
In mathematics, in particular abstract algebra, a graded algebra is an algebra over a field with an extra piece of structure, known as a gradation ....
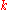 -algebra
-algebraAlgebra over a field
In mathematics, an algebra over a field is a vector space equipped with a bilinear vector product. That is to say, it isan algebraic structure consisting of a vector space together with an operation, usually called multiplication, that combines any two vectors to form a third vector; to qualify as...
over which the residue field
Residue field
In mathematics, the residue field is a basic construction in commutative algebra. If R is a commutative ring and m is a maximal ideal, then the residue field is the quotient ring k = R/m, which is a field...
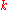 has a linear minimal graded free resolution, i.e., there exists an exact sequence
has a linear minimal graded free resolution, i.e., there exists an exact sequenceExact sequence
An exact sequence is a concept in mathematics, especially in homological algebra and other applications of abelian category theory, as well as in differential geometry and group theory...
:
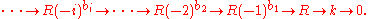
It is named after the French mathematician Jean-Louis Koszul
Jean-Louis Koszul
Jean-Louis Koszul is a mathematician best known for studying geometry and discovering the Koszul complex.He was educated at the Lycée Fustel-de-Coulanges in Strasbourg before studying at the Faculty of Science in Strasbourg and the Faculty of Science in Paris...
.
We can choose bases for the free modules in the resolution; then the maps can be written as matrices. For a Koszul algebra, the entries in the matrices are zero or linear forms.
An example of a Koszul algebra is a polynomial ring
Polynomial ring
In mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
over a field, for which the Koszul complex
Koszul complex
In mathematics, the Koszul complex was first introduced to define a cohomology theory for Lie algebras, by Jean-Louis Koszul...
is the minimal graded free resolution of the residue field. There are Koszul algebras whose residue fields have infinite minimal graded free resolutions, e.g,