QMA
Encyclopedia
In computational complexity theory
, QMA, which stands for Quantum Merlin Arthur, is the quantum analog of the deterministic complexity class NP
or the probabilistic complexity class MA. It is related to BQP
in the same way NP
is related to P
, or MA is related to BPP.
Informally, it is the set of decision problem
s for which when the answer is YES, there is a polynomial-size quantum proof (a quantum state) which convinces a polynomial-time quantum verifier of the fact with high probability. Moreover, when the answer is NO, every polynomial-size quantum state is rejected by the verifier with high probability.
More precisely, the proofs have to be verifiable in polynomial time on a quantum computer
, such that if the answer is indeed YES, the verifier accepts a correct proof with probability greater than 2/3, and if the answer is NO, then there is no proof which convinces the verifier to accept with probability greater than 1/3. As is usually the case, the constants 2/3 and 1/3 can be changed. Changing 2/3 to any constant strictly greater than 1/2 and 1/3 to any constant strictly lesser than 1/2 does not change the class QMA.
QAM is a related complexity class, where Arthur generates a random string, Merlin answers with a quantum certificate and Arthur verifies it as a BQP machine.
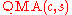if there exists a polynomial time quantum verifier V and a polynomial p(x) such that:
where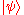
ranges over all quantum states with at most p(x) qubits.
The complexity class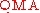
is defined to be equal to 
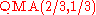. However, the constants are not too important since the class remains unchanged if 
and 
are set to any constants such that 
is greater than 
. Moreover, for any polynomials 
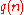and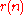 
, we have
.
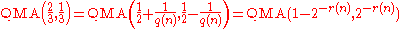A problem is said to be QMA-hard, analogous to NP-hard
, if every problem in QMA can be reduced
to it. A problem is said to be QMA-complete
if it is QMA-hard and in QMA.
. A Hamiltonian is a Hermitian matrix acting on quantum states, thus it is
for a system of n qubit
s. A k-local Hamiltonian is a Hamiltonian which can be written as the sum of Hamiltonians, each of which act non-trivially on at most k qubits (instead of all n qubits).
The k-local Hamiltonian problem, which is a promise problem
, is defined as follows. The input is a k-local Hamiltonian acting on n qubits, which is the sum of polynomially many Hermitian matrices that act on only k qubits. The input also contains two numbers
, such that 
for some constant c. The problem is to determine whether the smallest eigenvalue of this Hamiltonian is less than a or greater than b, promised that one of these is the case.
The k-local Hamiltonian is QMA-complete for k ≥ 2.
QMA-hardness results are known for even simplistic and physically realistic lattice models of qubits such as
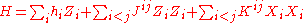
where
represent the Pauli matrices
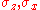. Such models are applicable to universal adiabatic quantum computation
.
The Hamiltonians for the QMA-complete problem can also be restricted to act on a two dimensional grid of qubits or a line of quantum particles with 12 states per particle.
QIP(k), which stands for Quantum Interactive Polynomial time (k messages), is a generalization of QMA where Merlin and Arthur can interact for k rounds. QMA is QIP(1). QIP(2) is known to be in PSPACE.
QIP is QIP(k) where k is allowed to be polynomial in the number of qubits. It is known that QIP(3) = QIP. It is also known that QIP = IP
= PSPACE
.
The first inclusion follows from the definition of NP
. The next two inclusions follow from the fact that the verifier is being made more powerful in each case. QCMA is contained in QMA since the verifier can force the prover to send a classical proof by measuring proofs as soon as they are received. The fact that QMA is contained in PP
was shown by Alexei Kitaev
and John Watrous. PP is also easily shown to be in PSPACE
.
It is unknown if any of these inclusions is strict. It is not even known whether P is strictly contained in PSPACE or P = PSPACE.
Computational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
, QMA, which stands for Quantum Merlin Arthur, is the quantum analog of the deterministic complexity class NP
NP (complexity)
In computational complexity theory, NP is one of the most fundamental complexity classes.The abbreviation NP refers to "nondeterministic polynomial time."...
or the probabilistic complexity class MA. It is related to BQP
BQP
In computational complexity theory BQP is the class of decision problems solvable by a quantum computer in polynomial time, with an error probability of at most 1/3 for all instances...
in the same way NP
NP (complexity)
In computational complexity theory, NP is one of the most fundamental complexity classes.The abbreviation NP refers to "nondeterministic polynomial time."...
is related to P
P (complexity)
In computational complexity theory, P, also known as PTIME or DTIME, is one of the most fundamental complexity classes. It contains all decision problems which can be solved by a deterministic Turing machine using a polynomial amount of computation time, or polynomial time.Cobham's thesis holds...
, or MA is related to BPP.
Informally, it is the set of decision problem
Decision problem
In computability theory and computational complexity theory, a decision problem is a question in some formal system with a yes-or-no answer, depending on the values of some input parameters. For example, the problem "given two numbers x and y, does x evenly divide y?" is a decision problem...
s for which when the answer is YES, there is a polynomial-size quantum proof (a quantum state) which convinces a polynomial-time quantum verifier of the fact with high probability. Moreover, when the answer is NO, every polynomial-size quantum state is rejected by the verifier with high probability.
More precisely, the proofs have to be verifiable in polynomial time on a quantum computer
Quantum computer
A quantum computer is a device for computation that makes direct use of quantum mechanical phenomena, such as superposition and entanglement, to perform operations on data. Quantum computers are different from traditional computers based on transistors...
, such that if the answer is indeed YES, the verifier accepts a correct proof with probability greater than 2/3, and if the answer is NO, then there is no proof which convinces the verifier to accept with probability greater than 1/3. As is usually the case, the constants 2/3 and 1/3 can be changed. Changing 2/3 to any constant strictly greater than 1/2 and 1/3 to any constant strictly lesser than 1/2 does not change the class QMA.
QAM is a related complexity class, where Arthur generates a random string, Merlin answers with a quantum certificate and Arthur verifies it as a BQP machine.
Definition
A language L is in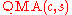 if there exists a polynomial time quantum verifier V and a polynomial p(x) such that:
, there exists a quantum state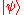 
such that the probability that V accepts the input 
is greater than 
.
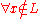, for all quantum states 
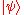, the probability that V accepts the input 
is less than 
.
where
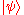ranges over all quantum states with at most p(x) qubits.The complexity class
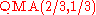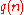is defined to be equal to . However, the constants are not too important since the class remains unchanged if and are set to any constants such that is greater than . Moreover, for any polynomials and 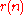, we have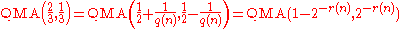.Problems in QMA
Since many interesting classes are contained in QMA, such as P, BQP and NP, all problems in those classes are also in QMA. However, there are problems that are in QMA but not known to be in NP or BQP. Some such well known problems are discussed below.A problem is said to be QMA-hard, analogous to NP-hard
NP-hard
NP-hard , in computational complexity theory, is a class of problems that are, informally, "at least as hard as the hardest problems in NP". A problem H is NP-hard if and only if there is an NP-complete problem L that is polynomial time Turing-reducible to H...
, if every problem in QMA can be reduced
Reduction (complexity)
In computability theory and computational complexity theory, a reduction is a transformation of one problem into another problem. Depending on the transformation used this can be used to define complexity classes on a set of problems....
to it. A problem is said to be QMA-complete
Complete (complexity)
In computational complexity theory, a computational problem is complete for a complexity class if it is, in a formal sense, one of the "hardest" or "most expressive" problems in the complexity class...
if it is QMA-hard and in QMA.
The local Hamiltonian problem
The local Hamiltonian problem is the quantum analogue of MAX-SATMaximum satisfiability problem
In computational complexity theory, the Maximum Satisfiability problem is the problem of determining the maximum number of clauses, of a given Boolean formula, that can be satisfied by some assignment...
. A Hamiltonian is a Hermitian matrix acting on quantum states, thus it is
for a system of n qubitQubit
In quantum computing, a qubit or quantum bit is a unit of quantum information—the quantum analogue of the classical bit—with additional dimensions associated to the quantum properties of a physical atom....
s. A k-local Hamiltonian is a Hamiltonian which can be written as the sum of Hamiltonians, each of which act non-trivially on at most k qubits (instead of all n qubits).
The k-local Hamiltonian problem, which is a promise problem
Promise problem
In computational complexity theory, a promise problem is a generalization of a decision problem where the input is promised to belong to a subset of all possible inputs. Unlike decision problems, the yes instances and no instances do not exhaust the set of all inputs...
, is defined as follows. The input is a k-local Hamiltonian acting on n qubits, which is the sum of polynomially many Hermitian matrices that act on only k qubits. The input also contains two numbers
, such that for some constant c. The problem is to determine whether the smallest eigenvalue of this Hamiltonian is less than a or greater than b, promised that one of these is the case.The k-local Hamiltonian is QMA-complete for k ≥ 2.
QMA-hardness results are known for even simplistic and physically realistic lattice models of qubits such as
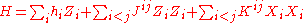
where
represent the Pauli matricesPauli matrices
The Pauli matrices are a set of three 2 × 2 complex matrices which are Hermitian and unitary. Usually indicated by the Greek letter "sigma" , they are occasionally denoted with a "tau" when used in connection with isospin symmetries...
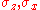. Such models are applicable to universal adiabatic quantum computationAdiabatic quantum computation
Adiabatic quantum computation relies on the adiabatic theorem to do calculations. First, a complex Hamiltonian is found whose ground state describes the solution to the problem of interest. Next, a system with a simple Hamiltonian is prepared and initialized to the ground state. Finally, the...
.
The Hamiltonians for the QMA-complete problem can also be restricted to act on a two dimensional grid of qubits or a line of quantum particles with 12 states per particle.
Related classes
QCMA (or MQA), which stands for Quantum Classical Merlin Arthur (or Merlin Quantum Arthur), is similar to QMA, but the proof has to be a classical string. It is not known whether QMA equals QCMA, although QCMA is clearly contained in QMA.QIP(k), which stands for Quantum Interactive Polynomial time (k messages), is a generalization of QMA where Merlin and Arthur can interact for k rounds. QMA is QIP(1). QIP(2) is known to be in PSPACE.
QIP is QIP(k) where k is allowed to be polynomial in the number of qubits. It is known that QIP(3) = QIP. It is also known that QIP = IP
IP (complexity)
In computational complexity theory, the class IP is the class of problems solvable by an interactive proof system. The concept of an interactive proof system was first introduced by Shafi Goldwasser, Silvio Micali, and Charles Rackoff in 1985...
= PSPACE
PSPACE
In computational complexity theory, PSPACE is the set of all decision problems which can be solved by a Turing machine using a polynomial amount of space.- Formal definition :...
.
Relationship to other classes
QMA is related to other known complexity classes by the following relations:The first inclusion follows from the definition of NP
NP (complexity)
In computational complexity theory, NP is one of the most fundamental complexity classes.The abbreviation NP refers to "nondeterministic polynomial time."...
. The next two inclusions follow from the fact that the verifier is being made more powerful in each case. QCMA is contained in QMA since the verifier can force the prover to send a classical proof by measuring proofs as soon as they are received. The fact that QMA is contained in PP
PP (complexity)
In complexity theory, PP is the class of decision problems solvable by a probabilistic Turing machine in polynomial time, with an error probability of less than 1/2 for all instances. The abbreviation PP refers to probabilistic polynomial time...
was shown by Alexei Kitaev
Alexei Kitaev
Alexei Kitaev is a professor of physics and computer science at the California Institute of Technology. He is best known for introducing the quantum phase estimation algorithm and the concept of the topological quantum computer while working at the Landau Institute for Theoretical Physics. For...
and John Watrous. PP is also easily shown to be in PSPACE
PSPACE
In computational complexity theory, PSPACE is the set of all decision problems which can be solved by a Turing machine using a polynomial amount of space.- Formal definition :...
.
It is unknown if any of these inclusions is strict. It is not even known whether P is strictly contained in PSPACE or P = PSPACE.