Adiabatic quantum computation
Encyclopedia
Adiabatic quantum computation (AQC) relies on the adiabatic theorem
to do calculations. First, a complex Hamiltonian
is found whose ground state describes the solution to the problem of interest. Next, a system with a simple Hamiltonian is prepared and initialized to the ground state. Finally, the simple Hamiltonian is adiabatically evolved to the complex Hamiltonian. By the adiabatic theorem, the system remains in the ground state, so at the end the state of the system describes the solution to the problem.
AQC is a possible method to get around the problem of energy relaxation
. Since the quantum system is in the ground state, interference with the outside world cannot make it move to a lower state. If the energy of the outside world (that is, the "temperature of the bath") is kept lower than the energy gap between the ground state and the next higher energy state, the system has a proportionally lower probability of going to a higher energy state. Thus the system can stay in a single system eigenstate as long as needed.
Universality results in the adiabatic model are tied to quantum complexity and QMA-hard problems. The k-local Hamiltonian is QMA-complete for k ≥ 2. QMA-hardness results are known for physically realistic lattice models of qubits such as
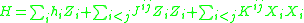
where
represent the Pauli matrices
. Such models are used for universal adiabatic quantum computation. The Hamiltonians for the QMA-complete problem can also be restricted to act on a two dimensional grid of qubits or a line of quantum particles with 12 states per particle. and if such models were found to be physically realisable, they too could be used to form the building blocks of a universal adiabatic quantum computer.
In practice, there are problems during a computation. As the Hamiltonian is gradually changed, the interesting parts (quantum behaviour as opposed to classical) occur when multiple qubit
s are close to a tipping point. It is exactly at this point when the ground state (one set of qubit orientations) gets very close to a first energy state (a different arrangement of orientations). Adding a slight amount of energy (from the external bath, or as a result of slowly changing the Hamiltonian) could take the system out of the ground state, and ruin the calculation. Trying to perform the calculation more quickly increases the external energy; scaling the number of qubits makes the energy gap at the tipping points smaller.
Adiabatic theorem
The adiabatic theorem is an important concept in quantum mechanics. Its original form, due to Max Born and Vladimir Fock , can be stated as follows:...
to do calculations. First, a complex Hamiltonian
Hamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
is found whose ground state describes the solution to the problem of interest. Next, a system with a simple Hamiltonian is prepared and initialized to the ground state. Finally, the simple Hamiltonian is adiabatically evolved to the complex Hamiltonian. By the adiabatic theorem, the system remains in the ground state, so at the end the state of the system describes the solution to the problem.
AQC is a possible method to get around the problem of energy relaxation
Quantum dissipation
Quantum Dissipation is the branch of physics that studies the quantum analogues of the process of irreversible loss of energy observed at the classical level. Its main purpose is to derive the laws of classical dissipation from the framework of quantum mechanics...
. Since the quantum system is in the ground state, interference with the outside world cannot make it move to a lower state. If the energy of the outside world (that is, the "temperature of the bath") is kept lower than the energy gap between the ground state and the next higher energy state, the system has a proportionally lower probability of going to a higher energy state. Thus the system can stay in a single system eigenstate as long as needed.
Universality results in the adiabatic model are tied to quantum complexity and QMA-hard problems. The k-local Hamiltonian is QMA-complete for k ≥ 2. QMA-hardness results are known for physically realistic lattice models of qubits such as
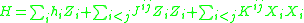
where
represent the Pauli matricesPauli matrices
The Pauli matrices are a set of three 2 × 2 complex matrices which are Hermitian and unitary. Usually indicated by the Greek letter "sigma" , they are occasionally denoted with a "tau" when used in connection with isospin symmetries...
. Such models are used for universal adiabatic quantum computation. The Hamiltonians for the QMA-complete problem can also be restricted to act on a two dimensional grid of qubits or a line of quantum particles with 12 states per particle. and if such models were found to be physically realisable, they too could be used to form the building blocks of a universal adiabatic quantum computer.In practice, there are problems during a computation. As the Hamiltonian is gradually changed, the interesting parts (quantum behaviour as opposed to classical) occur when multiple qubit
Qubit
In quantum computing, a qubit or quantum bit is a unit of quantum information—the quantum analogue of the classical bit—with additional dimensions associated to the quantum properties of a physical atom....
s are close to a tipping point. It is exactly at this point when the ground state (one set of qubit orientations) gets very close to a first energy state (a different arrangement of orientations). Adding a slight amount of energy (from the external bath, or as a result of slowly changing the Hamiltonian) could take the system out of the ground state, and ruin the calculation. Trying to perform the calculation more quickly increases the external energy; scaling the number of qubits makes the energy gap at the tipping points smaller.