
Pythagorean quadruple
Encyclopedia
A Pythagorean
quadruple is a tuple
of integer
s a, b, c and d, such that d > 0 and , and is often denoted
, and is often denoted  . Geometrically, a Pythagorean quadruple
. Geometrically, a Pythagorean quadruple  defines a cuboid
defines a cuboid
with side lengths |a|, |b|, and |c|, whose space diagonal
has integer length d. Pythagorean quadruples are thus also called Pythagorean Boxes.
of a, b, and c, is parametrized by,
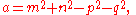
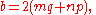
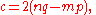
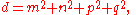
where m, n, p, q are integer
s. Thus, all primitive Pythagorean quadruples are characterized by the Lebesgue Identity

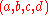 parametrized
parametrized
by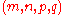 corresponds to the first column of the matrix representation
corresponds to the first column of the matrix representation 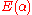 of conjugation
of conjugation  by the Hurwitz quaternion
by the Hurwitz quaternion
 restricted to the subspace of
restricted to the subspace of 
spanned by , which is given by
, which is given by
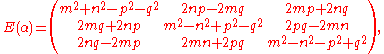
where the columns are pairwise orthogonal
and each have norm d. Furthermore, we have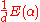
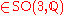
, and, in fact, all 3 × 3 orthogonal matrices with rational
coefficients arise in this manner.
Let p be any factor of , such that
, such that 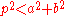 . Then
. Then 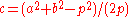 and
and  . Note that
. Note that  .
.
A similar method exists for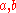 both even, with the further restriction that
both even, with the further restriction that 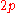 must be an even factor of
must be an even factor of  . No such method exists if both a and b are odd.
. No such method exists if both a and b are odd.
Pythagoras
Pythagoras of Samos was an Ionian Greek philosopher, mathematician, and founder of the religious movement called Pythagoreanism. Most of the information about Pythagoras was written down centuries after he lived, so very little reliable information is known about him...
quadruple is a tuple
Tuple
In mathematics and computer science, a tuple is an ordered list of elements. In set theory, an n-tuple is a sequence of n elements, where n is a positive integer. There is also one 0-tuple, an empty sequence. An n-tuple is defined inductively using the construction of an ordered pair...
of integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s a, b, c and d, such that d > 0 and
 , and is often denoted
, and is often denoted  . Geometrically, a Pythagorean quadruple
. Geometrically, a Pythagorean quadruple  defines a cuboid
defines a cuboidCuboid
In geometry, a cuboid is a solid figure bounded by six faces, forming a convex polyhedron. There are two competing definitions of a cuboid in mathematical literature...
with side lengths |a|, |b|, and |c|, whose space diagonal
Space diagonal
In a rectangular box or a magic cube, the four space diagonals are the lines that go from a corner of the box or cube, through the center of the box or cube, to the opposite corner...
has integer length d. Pythagorean quadruples are thus also called Pythagorean Boxes.
Parametrization of primitive quadruples
The set of all primitive Pythagorean quadruples, i.e., those for which gcd(a,b,c) = 1, where gcd denotes the greatest common divisorGreatest common divisor
In mathematics, the greatest common divisor , also known as the greatest common factor , or highest common factor , of two or more non-zero integers, is the largest positive integer that divides the numbers without a remainder.For example, the GCD of 8 and 12 is 4.This notion can be extended to...
of a, b, and c, is parametrized by,
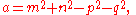
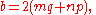
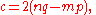
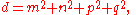
where m, n, p, q are integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s. Thus, all primitive Pythagorean quadruples are characterized by the Lebesgue Identity

Relationship with quaternions and rational orthogonal matrices
A primitive Pythagorean quadruple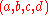 parametrized
parametrizedParametrization
Parametrization is the process of deciding and defining the parameters necessary for a complete or relevant specification of a model or geometric object....
by
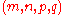 corresponds to the first column of the matrix representation
corresponds to the first column of the matrix representation 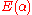 of conjugation
of conjugation  by the Hurwitz quaternion
by the Hurwitz quaternionHurwitz quaternion
In mathematics, a Hurwitz quaternion is a quaternion whose components are either all integers or all half-integers...
 restricted to the subspace of
restricted to the subspace of 
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
spanned by
 , which is given by
, which is given by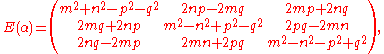
where the columns are pairwise orthogonal
Orthogonality
Orthogonality occurs when two things can vary independently, they are uncorrelated, or they are perpendicular.-Mathematics:In mathematics, two vectors are orthogonal if they are perpendicular, i.e., they form a right angle...
and each have norm d. Furthermore, we have
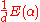
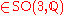
Orthogonal group
In mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
, and, in fact, all 3 × 3 orthogonal matrices with rational
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
coefficients arise in this manner.
Pythagorean quadruples with small norm
- (1,2,2,3), (2,3,6,7), (1,4,8,9), (4,4,7,9), (2,6,9,11), (6,6,7,11), (3,4,12,13), (2,5,14,15), (2, 10, 11, 15), (1,12,12,17), (8,9,12,17), (1,6,18,19), (6,6,17,19), (6,10,15,19), (4,5,20,21), (4,8,19,21), (4,13,16,21), (8,11,16,21), (3,6,22,23), (3,14,18,23), (6,13,18,23), (9, 12, 20, 25), (12, 15, 16, 25), (2,7,26,27), (2,10,25,27), (2,14,23,27), (7,14,22,27), (10,10,23,27), (3,16,24,29), (11,12,24,29), (12,16,21,29)
Alternate parametrization
All Pythagorean quadruples (including non-primitives, and with repetition, though a, b and c do not appear in all possible orders) can be generated from two positive integers a and b as follows:Let p be any factor of
 , such that
, such that 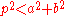 . Then
. Then 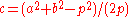 and
and  . Note that
. Note that  .
.A similar method exists for
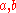 both even, with the further restriction that
both even, with the further restriction that 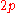 must be an even factor of
must be an even factor of  . No such method exists if both a and b are odd.
. No such method exists if both a and b are odd.See also
- Pythagorean triplePythagorean tripleA Pythagorean triple consists of three positive integers a, b, and c, such that . Such a triple is commonly written , and a well-known example is . If is a Pythagorean triple, then so is for any positive integer k. A primitive Pythagorean triple is one in which a, b and c are pairwise coprime...
- Quaternions and spatial rotationQuaternions and spatial rotationUnit quaternions provide a convenient mathematical notation for representing orientations and rotations of objects in three dimensions. Compared to Euler angles they are simpler to compose and avoid the problem of gimbal lock. Compared to rotation matrices they are more numerically stable and may...
- Euler-Rodrigues formula for 3D rotations

