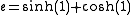Representations of e
Encyclopedia
The mathematical constant
e
can be represented in a variety of ways as a real number
. Since e is an irrational number
(see proof that e is irrational
), it cannot be represented as a fraction
, but it can be represented as a continued fraction
. Using calculus
, e may also be represented as an infinite series, infinite product, or other sort of limit of a sequence
.
proved that the number e is represented as the infinite simple continued fraction :
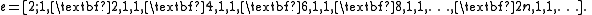
Its convergence can be tripled by allowing just one decimal number:
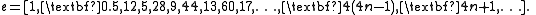
Here are some infinite generalized continued fraction
expansions of e. The second is generated from the first by a simple equivalence transformation. The last is equivalent to [1, 0.5, 12, 5, 28, 9, ...].
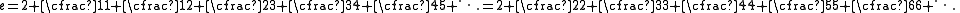
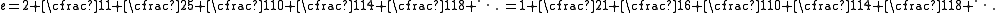
This last is a special case of a general formula for the exponential function
:
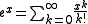for any real number x.
In the special case where x = 1, or −1, we have:
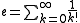, and
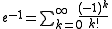
Other series are the following:
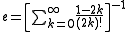
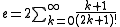
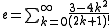
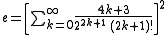
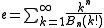where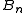 
is the 
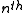Bell number
. Some few examples: (for n=1,2,3)
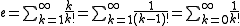
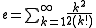
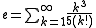
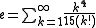
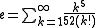
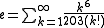
's product
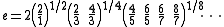
and Guillera's product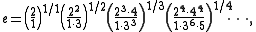
where the nth factor is the nth root of the product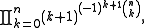
as well as the infinite product
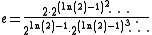
of several infinite sequences:
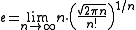and
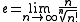(both by Stirling's formula).
The symmetric limit,
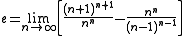
may be obtained by manipulation of the basic limit definition of e. Another limit is
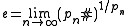
where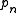
is the nth prime
and
is the primorial
of the nth prime.
Also: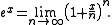
In the special case that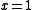
, the result is the famous statement:
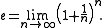
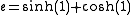
Mathematical constant
A mathematical constant is a special number, usually a real number, that is "significantly interesting in some way". Constants arise in many different areas of mathematics, with constants such as and occurring in such diverse contexts as geometry, number theory and calculus.What it means for a...
e
E (mathematical constant)
The mathematical constant ' is the unique real number such that the value of the derivative of the function at the point is equal to 1. The function so defined is called the exponential function, and its inverse is the natural logarithm, or logarithm to base...
can be represented in a variety of ways as a real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
. Since e is an irrational number
Irrational number
In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
(see proof that e is irrational
Proof that e is irrational
In mathematics, the series representation of Euler's number ecan be used to prove that e is irrational. Of the many representations of e, this is the Taylor series for the exponential function evaluated at y = 1.-Summary of the proof:...
), it cannot be represented as a fraction
Fraction (mathematics)
A fraction represents a part of a whole or, more generally, any number of equal parts. When spoken in everyday English, we specify how many parts of a certain size there are, for example, one-half, five-eighths and three-quarters.A common or "vulgar" fraction, such as 1/2, 5/8, 3/4, etc., consists...
, but it can be represented as a continued fraction
Continued fraction
In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on...
. Using calculus
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
, e may also be represented as an infinite series, infinite product, or other sort of limit of a sequence
Limit of a sequence
The limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
.
As a continued fraction
EulerLeonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
proved that the number e is represented as the infinite simple continued fraction :
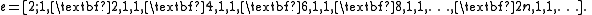
Its convergence can be tripled by allowing just one decimal number:
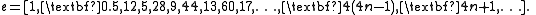
Here are some infinite generalized continued fraction
Generalized continued fraction
In complex analysis, a branch of mathematics, a generalized continued fraction is a generalization of regular continued fractions in canonical form, in which the partial numerators and partial denominators can assume arbitrary real or complex values....
expansions of e. The second is generated from the first by a simple equivalence transformation. The last is equivalent to [1, 0.5, 12, 5, 28, 9, ...].
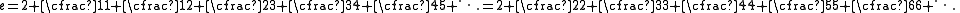
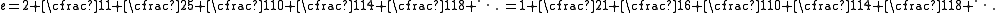
This last is a special case of a general formula for the exponential function
Exponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
:
As an infinite series
The number e can be expressed as the sum of the following infinite series: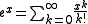 for any real number x.In the special case where x = 1, or −1, we have:
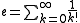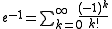
, andOther series are the following:
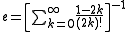
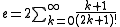
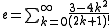
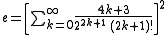
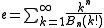where 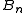is the 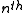Bell numberBell number
In combinatorics, the nth Bell number, named after Eric Temple Bell, is the number of partitions of a set with n members, or equivalently, the number of equivalence relations on it...
. Some few examples: (for n=1,2,3)
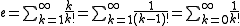
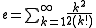
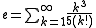
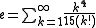
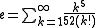
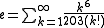
As an infinite product
The number e is also given by several infinite product forms including PippengerNick Pippenger
Nicholas John Pippenger is a researcher in computer science. He has produced a number of fundamental results many of which are being widely used in the field of theoretical computer science, database processing and compiler optimization. He has also achieved the rank of IBM Fellow at Almaden IBM...
's product
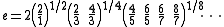
and Guillera's product
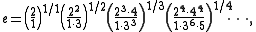
where the nth factor is the nth root of the product
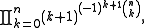
as well as the infinite product
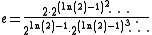
As the limit of a sequence
The number e is equal to the limitLimit of a sequence
The limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
of several infinite sequences:
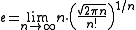and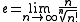 (both by Stirling's formula).The symmetric limit,
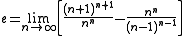
may be obtained by manipulation of the basic limit definition of e. Another limit is
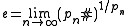
where
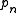is the nth primePrime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
and
is the primorialPrimorial
In mathematics, and more particularly in number theory, primorial is a function from natural numbers to natural numbers similar to the factorial function, but rather than multiplying successive positive integers, only successive prime numbers are multiplied...
of the nth prime.
Also:
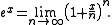
In the special case that
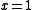, the result is the famous statement: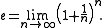In trigonometry
Trigonometrically, e can be written as the sum of two hyperbolic functions: