
Principal ideal theorem
Encyclopedia
In mathematics
, the principal ideal theorem of class field theory
, a branch of algebraic number theory
, is the statement that for any algebraic number field
K and any ideal I of the ring of integers
of K, if L is the Hilbert class field
of K, then
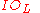
is a principal ideal
αOL, for OL the ring of integers of L and some element α in it. In other terms, extending ideals gives a mapping on the class group of K, to the class group of L, which sends all ideal classes to the class of a principal ideal. The phenomenon has also been called principalization, or sometimes capitulation. It was conjectured by David Hilbert
, and was the last remaining aspect of his programme on class fields to be completed, around 1930.
The question was reduced to a piece of finite group theory by Emil Artin
. That involved the transfer
. The required result was proved by Philipp Furtwängler
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the principal ideal theorem of class field theory
Class field theory
In mathematics, class field theory is a major branch of algebraic number theory that studies abelian extensions of number fields.Most of the central results in this area were proved in the period between 1900 and 1950...
, a branch of algebraic number theory
Algebraic number theory
Algebraic number theory is a major branch of number theory which studies algebraic structures related to algebraic integers. This is generally accomplished by considering a ring of algebraic integers O in an algebraic number field K/Q, and studying their algebraic properties such as factorization,...
, is the statement that for any algebraic number field
Algebraic number field
In mathematics, an algebraic number field F is a finite field extension of the field of rational numbers Q...
K and any ideal I of the ring of integers
Ring of integers
In mathematics, the ring of integers is the set of integers making an algebraic structure Z with the operations of integer addition, negation, and multiplication...
of K, if L is the Hilbert class field
Hilbert class field
In algebraic number theory, the Hilbert class field E of a number field K is the maximal abelian unramified extension of K. Its degree over K equals the class number of K and the Galois group of E over K is canonically isomorphic to the ideal class group of K using Frobenius elements for prime...
of K, then
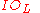
is a principal ideal
Principal ideal
In ring theory, a branch of abstract algebra, a principal ideal is an ideal I in a ring R that is generated by a single element a of R.More specifically:...
αOL, for OL the ring of integers of L and some element α in it. In other terms, extending ideals gives a mapping on the class group of K, to the class group of L, which sends all ideal classes to the class of a principal ideal. The phenomenon has also been called principalization, or sometimes capitulation. It was conjectured by David Hilbert
David Hilbert
David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
, and was the last remaining aspect of his programme on class fields to be completed, around 1930.
The question was reduced to a piece of finite group theory by Emil Artin
Emil Artin
Emil Artin was an Austrian-American mathematician of Armenian descent.-Parents:Emil Artin was born in Vienna to parents Emma Maria, née Laura , a soubrette on the operetta stages of Austria and Germany, and Emil Hadochadus Maria Artin, Austrian-born of Armenian descent...
. That involved the transfer
Transfer (group theory)
In mathematics, the transfer in group theory is a group homomorphism defined given a group G and a subgroup of finite index H, which goes from the abelianization of G to that of H.-Formulation:...
. The required result was proved by Philipp Furtwängler
Philipp Furtwängler
Philipp Furtwängler was a German number theorist.He wrote an 1896 doctoral dissertation at the University of Göttingen on cubic forms , under Felix Klein...
.

