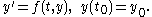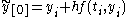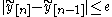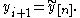Predictor-corrector method
Encyclopedia
In mathematics
, particularly numerical analysis
, a predictor–corrector method is an algorithm
that proceeds in two steps. First, the prediction step calculates a rough approximation of the desired quantity. Second, the corrector step refines the initial approximation using another means.
, suppose one knows the solution points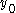 and
and 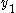 at times
at times 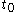 and
and 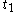 . By fitting a cubic polynomial to the points and their derivatives (obtained from the differential equation), one can predict a point
. By fitting a cubic polynomial to the points and their derivatives (obtained from the differential equation), one can predict a point 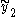 by extrapolating
by extrapolating
to a future time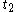 . Using the new value
. Using the new value 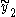 and its derivative there,
and its derivative there, 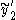 along with the previous points and their derivatives, one can then better interpolate
along with the previous points and their derivatives, one can then better interpolate
the derivative between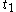 and
and 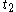 to get a better approximation
to get a better approximation 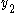 . The interpolation and subsequent integration of the differential equation constitute the corrector step.
. The interpolation and subsequent integration of the differential equation constitute the corrector step.
In this example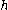 =
= 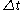 ,
, 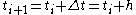
First calculate an initial guess value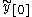 via Euler:
via Euler:
Next, improve the initial guess through iteration of the trapezoidal rule. This iteration process normally converges quickly.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, particularly numerical analysis
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
, a predictor–corrector method is an algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
that proceeds in two steps. First, the prediction step calculates a rough approximation of the desired quantity. Second, the corrector step refines the initial approximation using another means.
Example
In approximating the solution to a first-order ordinary differential equationOrdinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
, suppose one knows the solution points
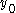 and
and 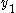 at times
at times 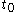 and
and 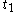 . By fitting a cubic polynomial to the points and their derivatives (obtained from the differential equation), one can predict a point
. By fitting a cubic polynomial to the points and their derivatives (obtained from the differential equation), one can predict a point 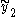 by extrapolating
by extrapolatingExtrapolation
In mathematics, extrapolation is the process of constructing new data points. It is similar to the process of interpolation, which constructs new points between known points, but the results of extrapolations are often less meaningful, and are subject to greater uncertainty. It may also mean...
to a future time
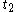 . Using the new value
. Using the new value 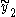 and its derivative there,
and its derivative there, 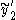 along with the previous points and their derivatives, one can then better interpolate
along with the previous points and their derivatives, one can then better interpolateInterpolation
In the mathematical field of numerical analysis, interpolation is a method of constructing new data points within the range of a discrete set of known data points....
the derivative between
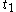 and
and 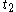 to get a better approximation
to get a better approximation 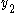 . The interpolation and subsequent integration of the differential equation constitute the corrector step.
. The interpolation and subsequent integration of the differential equation constitute the corrector step.Euler trapezoidal example
Example of an Euler – trapezoidal predictor–corrector method.In this example
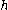 =
= 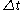 ,
, 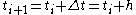
First calculate an initial guess value
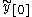 via Euler:
via Euler:Next, improve the initial guess through iteration of the trapezoidal rule. This iteration process normally converges quickly.
-
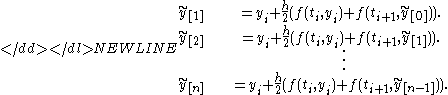
This iteration process is repeated until some fixed value n or until the guesses converge to within some error tolerance e :
then use the final guess as the next step:
Note that the overall error is unrelated to convergence in the algorithm but instead to the step size and the core method, which in this example is a trapezoidal, (linear) approximation of the actual function. The step size h (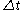 ) needs to be relatively small in order to get a good approximation. See also stiff equationStiff equationIn mathematics, a stiff equation is a differential equation for which certain numerical methods for solving the equation are numerically unstable, unless the step size is taken to be extremely small. It has proved difficult to formulate a precise definition of stiffness, but the main idea is that...
) needs to be relatively small in order to get a good approximation. See also stiff equationStiff equationIn mathematics, a stiff equation is a differential equation for which certain numerical methods for solving the equation are numerically unstable, unless the step size is taken to be extremely small. It has proved difficult to formulate a precise definition of stiffness, but the main idea is that...
.
See also
- Backward differentiation formulaBackward differentiation formulaThe backward differentiation formula is a family of implicit methods for the numerical integration of ordinary differential equations. They are linear multistep methods that, for a given function and time, approximate the derivative of that function using information from already computed times,...
- Beeman's algorithmBeeman's algorithmBeeman's algorithm is a method for numerically integrating ordinary differential equations of order 2, more specifically Newton's equations of motion \ddot x=A. It was designed to allow high numbers of particles in simulations of molecular dynamics. There is a direct or explicit and an implicit...
- Heun's methodHeun's methodIn mathematics and computational science, Heun's method may refer to the improved or modified Euler's method , or a similar two-stage Runge–Kutta method. It is named after Karl L. W. M. Heun and is a numerical procedure for solving ordinary differential equations with a given initial value...
- Mehrotra predictor–corrector method
- Numerical continuationNumerical continuationNumerical continuation is a method of computing approximate solutions of a system of parameterized nonlinear equations,F = 0The parameter \lambda is usually a real scalar, and the solution an n-vector...
External links
- Predictor–corrector methods for differential equations
-