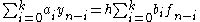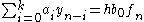Backward differentiation formula
Encyclopedia
The backward differentiation formula (BDF) is a family of implicit methods for the numerical integration of ordinary differential equations
. They are linear multistep methods that, for a given function and time, approximate the derivative of that function using information from already computed times, thereby increasing the accuracy of the approximation. These methods are especially used for the solution of stiff differential equations
.
BDFs are a kind of linear multistep method that are particularly useful for stiff equations
. The general formula for a linear mulitistep method can be written as
where h denotes the step size,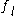 denotes
denotes  , and the coefficients,
, and the coefficients, 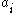 and
and 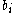 , determine the particular linear multistep method. The family of BDFs consist of the methods arising from the case
, determine the particular linear multistep method. The family of BDFs consist of the methods arising from the case 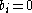 for
for 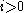 . The general formula for a BDF can be written as
. The general formula for a BDF can be written as
BDF methods are implicit and, as such, require the solution of non-linear equations at each step. Typically, a modified Newton's method
is used to solve these non-linear equations.
Numerical ordinary differential equations
Numerical ordinary differential equations is the part of numerical analysis which studies the numerical solution of ordinary differential equations...
. They are linear multistep methods that, for a given function and time, approximate the derivative of that function using information from already computed times, thereby increasing the accuracy of the approximation. These methods are especially used for the solution of stiff differential equations
Stiff equation
In mathematics, a stiff equation is a differential equation for which certain numerical methods for solving the equation are numerically unstable, unless the step size is taken to be extremely small. It has proved difficult to formulate a precise definition of stiffness, but the main idea is that...
.
General formula
A BDF is used to solve the initial value problemInitial value problem
In mathematics, in the field of differential equations, an initial value problem is an ordinary differential equation together with a specified value, called the initial condition, of the unknown function at a given point in the domain of the solution...
BDFs are a kind of linear multistep method that are particularly useful for stiff equations
Stiff equation
In mathematics, a stiff equation is a differential equation for which certain numerical methods for solving the equation are numerically unstable, unless the step size is taken to be extremely small. It has proved difficult to formulate a precise definition of stiffness, but the main idea is that...
. The general formula for a linear mulitistep method can be written as
where h denotes the step size,
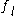 denotes
denotes  , and the coefficients,
, and the coefficients, 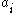 and
and 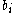 , determine the particular linear multistep method. The family of BDFs consist of the methods arising from the case
, determine the particular linear multistep method. The family of BDFs consist of the methods arising from the case 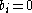 for
for 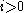 . The general formula for a BDF can be written as
. The general formula for a BDF can be written as BDF methods are implicit and, as such, require the solution of non-linear equations at each step. Typically, a modified Newton's method
Newton's method
In numerical analysis, Newton's method , named after Isaac Newton and Joseph Raphson, is a method for finding successively better approximations to the roots of a real-valued function. The algorithm is first in the class of Householder's methods, succeeded by Halley's method...
is used to solve these non-linear equations.