
Polynomial SOS
Encyclopedia
In mathematics
, a form
(i.e. a homogeneous polynomial) h(x) of degree 2m in the real n-dimensional vector x is sum of squares of forms (SOS) if and only if there exist forms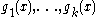 of degree m such that
of degree m such that
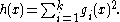
Explicit sufficient conditions for a form to be SOS have been found. However every real nonnegative form can be approximated as closely as desired (in the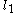 -norm of its coefficient vector) by a sequence of forms
-norm of its coefficient vector) by a sequence of forms  that are SOS.
that are SOS.
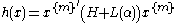
where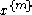 is a vector containing a base for the forms of degree m in x (such as all monomials of degree m in x), the prime ′ denotes the transpose
is a vector containing a base for the forms of degree m in x (such as all monomials of degree m in x), the prime ′ denotes the transpose
, H is any symmetric matrix satisfying
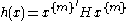
and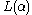 is a linear parameterization of the linear space
is a linear parameterization of the linear space
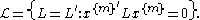
The dimension of the vector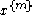 is given by
is given by

whereas the dimension of the vector is given by
is given by
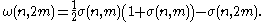
Then, h(x) is SOS if and only if there exists a vector such that
such that
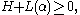
meaning that the matrix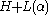 is positive-semidefinite. This is a linear matrix inequality (LMI) feasibility test, which is a convex optimization problem. The expression
is positive-semidefinite. This is a linear matrix inequality (LMI) feasibility test, which is a convex optimization problem. The expression 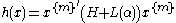 was introduced in [1] with the name square matricial representation (SMR) in order to establish whether a form is SOS via an LMI. This representation is also known as Gram matrix (see [2] and references therein).
was introduced in [1] with the name square matricial representation (SMR) in order to establish whether a form is SOS via an LMI. This representation is also known as Gram matrix (see [2] and references therein).
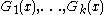 of degree m such that
of degree m such that
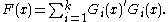
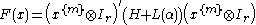
where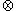 is the Kronecker product
is the Kronecker product
of matrices, H is any symmetric matrix satisfying
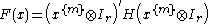
and is a linear parameterization of the linear space
is a linear parameterization of the linear space
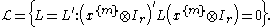
The dimension of the vector is given by
is given by
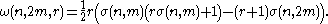
Then, F(x) is SOS if and only if there exists a vector such that the following LMI holds:
such that the following LMI holds:
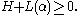
The expression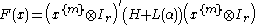 was introduced in [3] in order to establish whether a matrix form is SOS via an LMI.
was introduced in [3] in order to establish whether a matrix form is SOS via an LMI.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a form
Homogeneous polynomial
In mathematics, a homogeneous polynomial is a polynomial whose monomials with nonzero coefficients all have thesame total degree. For example, x^5 + 2 x^3 y^2 + 9 x y^4 is a homogeneous polynomial...
(i.e. a homogeneous polynomial) h(x) of degree 2m in the real n-dimensional vector x is sum of squares of forms (SOS) if and only if there exist forms
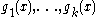 of degree m such that
of degree m such that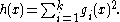
Explicit sufficient conditions for a form to be SOS have been found. However every real nonnegative form can be approximated as closely as desired (in the
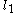 -norm of its coefficient vector) by a sequence of forms
-norm of its coefficient vector) by a sequence of forms  that are SOS.
that are SOS.Square matricial representation (SMR)
To establish whether a form h(x) is SOS amounts to solving a convex optimization problem. Indeed, any h(x) can be written as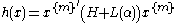
where
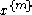 is a vector containing a base for the forms of degree m in x (such as all monomials of degree m in x), the prime ′ denotes the transpose
is a vector containing a base for the forms of degree m in x (such as all monomials of degree m in x), the prime ′ denotes the transposeTranspose
In linear algebra, the transpose of a matrix A is another matrix AT created by any one of the following equivalent actions:...
, H is any symmetric matrix satisfying
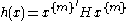
and
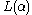 is a linear parameterization of the linear space
is a linear parameterization of the linear spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
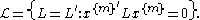
The dimension of the vector
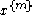 is given by
is given by
whereas the dimension of the vector
 is given by
is given by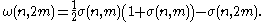
Then, h(x) is SOS if and only if there exists a vector
 such that
such that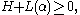
meaning that the matrix
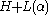 is positive-semidefinite. This is a linear matrix inequality (LMI) feasibility test, which is a convex optimization problem. The expression
is positive-semidefinite. This is a linear matrix inequality (LMI) feasibility test, which is a convex optimization problem. The expression 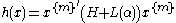 was introduced in [1] with the name square matricial representation (SMR) in order to establish whether a form is SOS via an LMI. This representation is also known as Gram matrix (see [2] and references therein).
was introduced in [1] with the name square matricial representation (SMR) in order to establish whether a form is SOS via an LMI. This representation is also known as Gram matrix (see [2] and references therein).Examples
- Consider the form of degree 4 in two variables
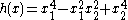 . We have
. We have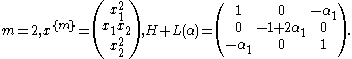
Since there exists α such that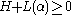 , namely
, namely 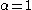 , it follows that h(x) is SOS.
, it follows that h(x) is SOS.
- Consider the form of degree 4 in three variables
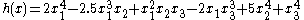 . We have
. We have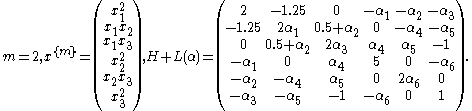
Since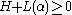 for
for  , it follows that h(x) is SOS.
, it follows that h(x) is SOS.
Matrix SOS
A matrix form F(x) (i.e., a matrix whose entries are forms) of dimension r and degree 2m in the real n-dimensional vector x is SOS if and only if there exist matrix forms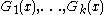 of degree m such that
of degree m such that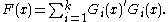
Matrix SMR
To establish whether a matrix form F(x) is SOS amounts to solving a convex optimization problem. Indeed, similarly to the scalar case any F(x) can be written according to the SMR as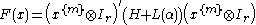
where
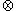 is the Kronecker product
is the Kronecker productKronecker product
In mathematics, the Kronecker product, denoted by ⊗, is an operation on two matrices of arbitrary size resulting in a block matrix. It gives the matrix of the tensor product with respect to a standard choice of basis. The Kronecker product should not be confused with the usual matrix...
of matrices, H is any symmetric matrix satisfying
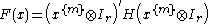
and
 is a linear parameterization of the linear space
is a linear parameterization of the linear space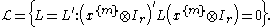
The dimension of the vector
 is given by
is given by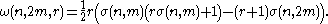
Then, F(x) is SOS if and only if there exists a vector
 such that the following LMI holds:
such that the following LMI holds: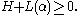
The expression
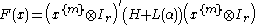 was introduced in [3] in order to establish whether a matrix form is SOS via an LMI.
was introduced in [3] in order to establish whether a matrix form is SOS via an LMI.

