In convex optimization, a linear matrix inequality (LMI) is an expression of the form

where

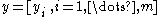• is a real vector,
• are 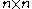symmetric matrices ,
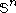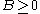• is a generalized inequality meaning 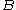is a positive semidefinite matrix belonging to the positive semidefinite cone 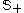in the subspace of symmetric matrices .

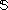This linear matrix inequality specifies a convex

Convex set

In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...

 constraint on y.

Applications

There are efficient numerical methods to determine whether an LMI is feasible (e.g., whether there exists a vector y such that LMI(y) ≥ 0), or to solve a convex optimization problem with LMI constraints.
Many optimization problems in control theory

Control theory

Control theory is an interdisciplinary branch of engineering and mathematics that deals with the behavior of dynamical systems. The desired output of a system is called the reference...

, system identification

System identification

In control engineering, the field of system identification uses statistical methods to build mathematical models of dynamical systems from measured data...

 and signal processing

Signal processing

Signal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...

 can be formulated using LMIs. Also LMIs find application in Polynomial Sum-Of-Squares

Polynomial SOS

In mathematics, a form h of degree 2m in the real n-dimensional vector x is sum of squares of forms if and only if there exist forms g_1,\ldots,g_k of degree m such that...

. The prototypical primal and dual semidefinite program

Semidefinite programming

Semidefinite programming is a subfield of convex optimization concerned with the optimization of a linear objective functionover the intersection of the cone of positive semidefinite matrices with an affine space, i.e., a spectrahedron....

 is a minimization of a real linear function respectively subject to the primal and dual convex cone

Convex cone

In linear algebra, a convex cone is a subset of a vector space over an ordered field that is closed under linear combinations with positive coefficients.-Definition:...

s governing this LMI.

Solving LMIs

A major breakthrough in convex optimization lies in the introduction of interior-point methods. These methods were developed in a series of papers and became of true interest in the context of LMI problems in the work of Yurii Nesterov and Arkadii Nemirovskii.

External links

• S. Boyd, L. El Ghaoui, E. Feron, and V. Balakrishnan, Linear Matrix Inequalities in System and Control Theory (book in pdf)

• C. Scherer and S. Weiland Course on Linear Matrix Inequalities in Control, Dutch Institute of Systems and Control (DISC).