
Polymatroid
Encyclopedia
In mathematics, polymatroid is a polytope associated with a submodular function. The notion was introduced by Jack Edmonds
in 1970.
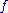 on
on 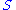 . Then define two associated polyhedra.
. Then define two associated polyhedra.
Here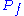 is called the polymatroid and
is called the polymatroid and 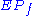 is called the extended polymatroid associated with
is called the extended polymatroid associated with 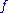 .
.
Jack Edmonds
Jack R. Edmonds is a mathematician, regarded as one of the most important contributors to the field of combinatorial optimization...
in 1970.
Definition
Consider any submodular set function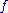 on
on 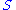 . Then define two associated polyhedra.
. Then define two associated polyhedra.
-
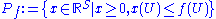 for each
for each 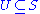
-
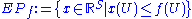 for each
for each 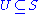
Here
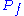 is called the polymatroid and
is called the polymatroid and 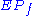 is called the extended polymatroid associated with
is called the extended polymatroid associated with 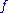 .
.Properties
-
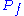 is nonempty if and only if
is nonempty if and only if  and that
and that 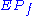 is nonempty if and only if
is nonempty if and only if 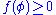
- Given any extended polymatroid
 there is a unique submodular function
there is a unique submodular function 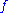 such that
such that 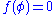 and
and 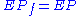
- If r is integral, 1-LipschitzLipschitz continuityIn mathematical analysis, Lipschitz continuity, named after Rudolf Lipschitz, is a strong form of uniform continuity for functions. Intuitively, a Lipschitz continuous function is limited in how fast it can change: for every pair of points on the graph of this function, the absolute value of the...
, and then r is the rank-function of a matroid, and the polymatroid is the independent set polytope, so-called since Edmonds showed it is the convex hullConvex hullIn mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....
then r is the rank-function of a matroid, and the polymatroid is the independent set polytope, so-called since Edmonds showed it is the convex hullConvex hullIn mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....
of the characteristic vectors of all independent sets of the matroid. - For a supermodularSupermodularIn mathematics, a functionf\colon R^k \to Ris supermodular iff + f \geq f + ffor all x, y \isin Rk, where x \vee y denotes the componentwise maximum and x \wedge y the componentwise minimum of x and y.If −f is supermodular then f is called submodular, and if the inequality is changed to an...
f one analogously may define the contrapolymatroid
-
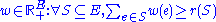
- This analogously generalizes the dominant of the spanning set polytopePolytopeIn elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...
of matroids.

