Supermodular
Encyclopedia
In mathematics
, a function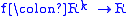
is supermodular if
for all x, y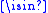
Rk, where x 
y denotes the componentwise maximum and x 
y the componentwise minimum of x and y.
If −f is supermodular then f is called submodular, and if the inequality is changed to an equality the function is modular.
If f is twice continuously differentiable, then supermodularity is equivalent to the condition
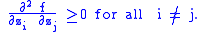
decision affects the incentives of others.
Consider a symmetric game
with a smooth payoff function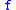
defined over actions 
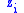of two or more players 
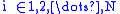. Suppose the action space is continuous; for simplicity, suppose each action is chosen from an interval: 
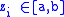. In this context, supermodularity of 
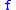implies that an increase in player 
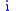's choice 
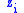increases the marginal payoff 
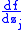of action 
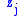for all other players 
. That is, if any player 
chooses a higher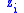 
, all other players 
have an incentive to raise their choices 
too. Following the terminology of Bulow, Geanakoplos, and Klemperer (1985), economists call this situation strategic complementarity
, because players' strategies are complements to each other. This is the basic property underlying examples of multiple equilibria in coordination game
s.
The opposite case of submodularity of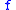
corresponds to the situation of strategic substitutability
. An increase in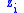
lowers the marginal payoff to all other player's choices 
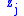, so strategies are substitutes. That is, if 
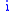chooses a higher 
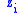, other players have an incentive to pick a lower 
.
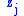For example, Bulow et al. consider the interactions of many imperfectly competitive
firms. When an increase in output by one firm raises the marginal revenues of the other firms, production decisions are strategic complements. When an increase in output by one firm lowers the marginal revenues of the other firms, production decisions are strategic substitutes.
A standard reference on the subject is by Topkis.
Let S be a finite set. A function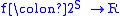
is submodular if for any 
and 
, 
. For supermodularity, the inequality is reversed.
A simple illustration example motivates this definition of submodular. Let S be a set of different foods,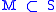
a meal, and 
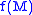the "goodness" of that meal. Then A above is one meal, and B is A but with even more options. Let x be ice cream. Adding ice cream to a meal is always good, but it is best if there is not already a dessert. If A and B either both have a dessert or both do not, then adding ice cream to them is comparably good. But if A does not have dessert and B does, then the effect of adding ice cream is more pronounced in A.
The definition of submodularity can equivalently be formulated as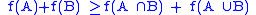
for all subsets A and B of S.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a function
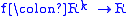
is supermodular if
for all x, y
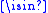Rk, where x y denotes the componentwise maximum and x y the componentwise minimum of x and y.If −f is supermodular then f is called submodular, and if the inequality is changed to an equality the function is modular.
If f is twice continuously differentiable, then supermodularity is equivalent to the condition
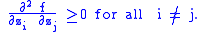
Supermodularity in economics and game theory
The concept of supermodularity is used in the social sciences to analyze how one agent'sAgent (economics)
In economics, an agent is an actor and decision maker in a model. Typically, every agent makes decisions by solving a well or ill defined optimization/choice problem. The term agent can also be seen as equivalent to player in game theory....
decision affects the incentives of others.
Consider a symmetric game
Symmetric game
In game theory, a symmetric game is a game where the payoffs for playing a particular strategy depend only on the other strategies employed, not on who is playing them. If one can change the identities of the players without changing the payoff to the strategies, then a game is symmetric. ...
with a smooth payoff function
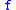defined over actions 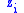of two or more players 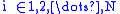. Suppose the action space is continuous; for simplicity, suppose each action is chosen from an interval: 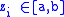. In this context, supermodularity of 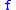implies that an increase in player 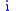's choice 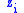increases the marginal payoff 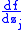of action 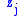for all other players . That is, if any player chooses a higher 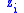, all other players have an incentive to raise their choices too. Following the terminology of Bulow, Geanakoplos, and Klemperer (1985), economists call this situation strategic complementarityStrategic complements
In economics and game theory, the decisions of two or more players are called strategic complements if they mutually reinforce one another, and they are called strategic substitutes if they mutually offset one another...
, because players' strategies are complements to each other. This is the basic property underlying examples of multiple equilibria in coordination game
Coordination game
In game theory, coordination games are a class of games with multiple pure strategy Nash equilibria in which players choose the same or corresponding strategies...
s.
The opposite case of submodularity of
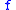corresponds to the situation of strategic substitutabilityStrategic complements
In economics and game theory, the decisions of two or more players are called strategic complements if they mutually reinforce one another, and they are called strategic substitutes if they mutually offset one another...
. An increase in
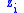lowers the marginal payoff to all other player's choices 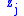, so strategies are substitutes. That is, if 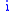chooses a higher 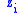, other players have an incentive to pick a lower 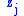.For example, Bulow et al. consider the interactions of many imperfectly competitive
Imperfect competition
In economic theory, imperfect competition is the competitive situation in any market where the conditions necessary for perfect competition are not satisfied...
firms. When an increase in output by one firm raises the marginal revenues of the other firms, production decisions are strategic complements. When an increase in output by one firm lowers the marginal revenues of the other firms, production decisions are strategic substitutes.
A standard reference on the subject is by Topkis.
Supermodular functions of subsets
Supermodularity and submodularity are also defined for functions defined over subsets of a larger set. Intuitively, a submodular function over the subsets demonstrates "diminishing returns". There are specialized techniques for optimizing submodular functions.Let S be a finite set. A function
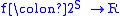is submodular if for any and , . For supermodularity, the inequality is reversed.A simple illustration example motivates this definition of submodular. Let S be a set of different foods,
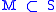a meal, and 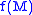the "goodness" of that meal. Then A above is one meal, and B is A but with even more options. Let x be ice cream. Adding ice cream to a meal is always good, but it is best if there is not already a dessert. If A and B either both have a dessert or both do not, then adding ice cream to them is comparably good. But if A does not have dessert and B does, then the effect of adding ice cream is more pronounced in A.The definition of submodularity can equivalently be formulated as
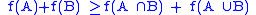
for all subsets A and B of S.