
Photon sphere
Encyclopedia
A photon sphere is a spherical region of space where gravity is strong enough that photons are forced to travel in orbits. The minimum radius for a stable orbit is:
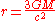
The radius for the photon sphere is
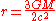
or in other words, one and a half times the Schwarzschild Radius.
This equation entails that photon spheres can only exist in the space surrounding an extremely compact object, such as a black hole
or a neutron star
.
As photons travel near the event horizon
of a black hole they can escape being pulled in by the gravity of a black hole by traveling at a nearly vertical direction known as an exit cone. A photon on the boundary of this cone will not completely escape the gravity of the black hole. Instead it orbits the black hole. These orbits are not stable.
The photon sphere is located farther from the center of a black hole than the event horizon and ergosphere
. Within a photon sphere it is possible to imagine a photon
that starts at the back of your head and orbits around a black hole only then be seen by your eyes.
For non-rotating black holes, the photon sphere is a sphere of radius
3/2 Rs, where Rs denotes the Schwarzschild radius
(the radius of the event horizon) - see below for a derivation of this result. No unaccelerated orbit with a semi-major axis
less than this distance is possible, but within the photon sphere, a constant acceleration will allow a spacecraft or probe to hover above the event horizon.
A rotating black hole
has two photon spheres. As a black hole rotates, it drags space with it. The photon sphere that is closer to the black hole is moving in the same direction as the rotation, whereas the photon sphere further away is moving against it. The greater the angular velocity
of the rotation of a black hole the greater distance between the two photon spheres. Because the black hole has an axis of rotation this only holds true if approaching the black hole in the direction of the equator. If approaching at a different angle, such as one from the poles of the black hole to the equator, there is only one photon sphere. This is because approaching at this angle the possibility of traveling with or against the rotation does not exist.
This derivation involves using the Schwarzschild metric
, given by:

For a photon travelling at a constant radius r (i.e. in the Φ-coordinate direction), ds, dr and dθ all must equal zero (the consequence of ds = 0 is a "light-like interval").
Setting ds, dr and dθ to zero, we have:
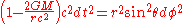
Re-arranging gives:
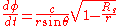
where Rs is the Schwarzschild radius.
The thing we shall know to proceed is the relation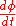 . To find it we should use radial geodesic equation
. To find it we should use radial geodesic equation
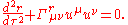
Not null -connection coefficients are
-connection coefficients are 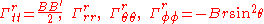 , where
, where 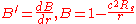 .
.
We treat photon radial geodesic with constant r and , therefore
, therefore
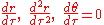 .
.
Putting it all into r-geodesic equation we obtain
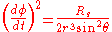
Comparing it with obtained previously, we have:
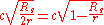
where we have inserted radians (imagine that the central mass, about which the photon is orbitting, is located at the centre of the coordinate axes. Then, as the photon is travelling along the
radians (imagine that the central mass, about which the photon is orbitting, is located at the centre of the coordinate axes. Then, as the photon is travelling along the  -coordinate line, for the mass to be located directly in the centre of the photon's orbit, we must have
-coordinate line, for the mass to be located directly in the centre of the photon's orbit, we must have 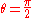 radians).
radians).
Hence, rearranging this final expression gives:

which is the result we set out to prove.
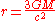
The radius for the photon sphere is
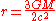
or in other words, one and a half times the Schwarzschild Radius.
This equation entails that photon spheres can only exist in the space surrounding an extremely compact object, such as a black hole
Black hole
A black hole is a region of spacetime from which nothing, not even light, can escape. The theory of general relativity predicts that a sufficiently compact mass will deform spacetime to form a black hole. Around a black hole there is a mathematically defined surface called an event horizon that...
or a neutron star
Neutron star
A neutron star is a type of stellar remnant that can result from the gravitational collapse of a massive star during a Type II, Type Ib or Type Ic supernova event. Such stars are composed almost entirely of neutrons, which are subatomic particles without electrical charge and with a slightly larger...
.
As photons travel near the event horizon
Event horizon
In general relativity, an event horizon is a boundary in spacetime beyond which events cannot affect an outside observer. In layman's terms it is defined as "the point of no return" i.e. the point at which the gravitational pull becomes so great as to make escape impossible. The most common case...
of a black hole they can escape being pulled in by the gravity of a black hole by traveling at a nearly vertical direction known as an exit cone. A photon on the boundary of this cone will not completely escape the gravity of the black hole. Instead it orbits the black hole. These orbits are not stable.
The photon sphere is located farther from the center of a black hole than the event horizon and ergosphere
Ergosphere
The ergosphere is a region located outside a rotating black hole. Its name is derived from the Greek word ergon, which means “work”. It received this name because it is theoretically possible to extract energy and mass from the black hole in this region...
. Within a photon sphere it is possible to imagine a photon
Photon
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
that starts at the back of your head and orbits around a black hole only then be seen by your eyes.
For non-rotating black holes, the photon sphere is a sphere of radius
Radius
In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...
3/2 Rs, where Rs denotes the Schwarzschild radius
Schwarzschild radius
The Schwarzschild radius is the distance from the center of an object such that, if all the mass of the object were compressed within that sphere, the escape speed from the surface would equal the speed of light...
(the radius of the event horizon) - see below for a derivation of this result. No unaccelerated orbit with a semi-major axis
Semi-major axis
The major axis of an ellipse is its longest diameter, a line that runs through the centre and both foci, its ends being at the widest points of the shape...
less than this distance is possible, but within the photon sphere, a constant acceleration will allow a spacecraft or probe to hover above the event horizon.
A rotating black hole
Rotating black hole
A rotating black hole is a black hole that possesses spin angular momentum.-Types of black holes:There are four known, exact, black hole solutions to Einstein's equations, which describe gravity in General Relativity. Two of these rotate...
has two photon spheres. As a black hole rotates, it drags space with it. The photon sphere that is closer to the black hole is moving in the same direction as the rotation, whereas the photon sphere further away is moving against it. The greater the angular velocity
Angular velocity
In physics, the angular velocity is a vector quantity which specifies the angular speed of an object and the axis about which the object is rotating. The SI unit of angular velocity is radians per second, although it may be measured in other units such as degrees per second, revolutions per...
of the rotation of a black hole the greater distance between the two photon spheres. Because the black hole has an axis of rotation this only holds true if approaching the black hole in the direction of the equator. If approaching at a different angle, such as one from the poles of the black hole to the equator, there is only one photon sphere. This is because approaching at this angle the possibility of traveling with or against the rotation does not exist.
Derivation for a Schwarzschild black hole
Since a Schwarzschild black hole has spherical symmetry, all possible axes for a circular photon orbit are equivalent, and all circular orbits have the same radius.This derivation involves using the Schwarzschild metric
Schwarzschild metric
In Einstein's theory of general relativity, the Schwarzschild solution describes the gravitational field outside a spherical, uncharged, non-rotating mass such as a star, planet, or black hole. It is also a good approximation to the gravitational field of a slowly rotating body like the Earth or...
, given by:

For a photon travelling at a constant radius r (i.e. in the Φ-coordinate direction), ds, dr and dθ all must equal zero (the consequence of ds = 0 is a "light-like interval").
Setting ds, dr and dθ to zero, we have:
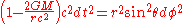
Re-arranging gives:
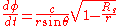
where Rs is the Schwarzschild radius.
The thing we shall know to proceed is the relation
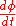 . To find it we should use radial geodesic equation
. To find it we should use radial geodesic equation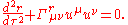
Not null
 -connection coefficients are
-connection coefficients are 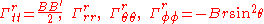 , where
, where 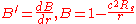 .
.We treat photon radial geodesic with constant r and
 , therefore
, therefore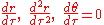 .
.Putting it all into r-geodesic equation we obtain
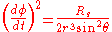
Comparing it with obtained previously, we have:
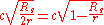
where we have inserted
 radians (imagine that the central mass, about which the photon is orbitting, is located at the centre of the coordinate axes. Then, as the photon is travelling along the
radians (imagine that the central mass, about which the photon is orbitting, is located at the centre of the coordinate axes. Then, as the photon is travelling along the  -coordinate line, for the mass to be located directly in the centre of the photon's orbit, we must have
-coordinate line, for the mass to be located directly in the centre of the photon's orbit, we must have 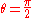 radians).
radians).Hence, rearranging this final expression gives:

which is the result we set out to prove.
Spherical photon orbits around a Kerr black hole
In contrast to a Schwarzschild black hole, a Kerr (spinning) black hole does not have spherical symmetry, but only an axis of symmetry, which has profound consequences for the photon orbits. A circular orbit can only exist in the equatorial plane, and there are two of them (prograde and retrograde), with different radii. All other constant-radius orbits have more complicated paths that oscillate in latitude about the equator.

