
Perturbation function
Encyclopedia
In mathematical optimization, the perturbation function is any function
which relates to primal and dual problem
s. The name comes from the fact that any such function defines a perturbation of the initial problem. In many cases this takes the form of shifting the constraints.
In some texts the value function is called the perturbation function, and the perturbation function is called the bifunction.
s separated locally convex spaces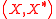 and
and  . Then given the function
. Then given the function 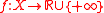 , we can define the primal problem by
, we can define the primal problem by
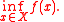
If there are constraint conditions, these can be built in to the function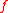 by letting
by letting  where
where 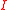 is the indicator function
is the indicator function
. Then is a perturbation function if and only if
is a perturbation function if and only if 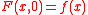 .
.
is the difference of the right and left hand side of the inequality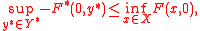
where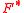 is the convex conjugate
is the convex conjugate
in both variables.
For any choice of perturbation function F weak duality holds. There are a number of conditions which if satisfied imply strong duality. For instance, if F is proper
, jointly convex
, lower semi-continuous with (where
(where  is the algebraic interior
is the algebraic interior
and is the projection onto Y defined by
is the projection onto Y defined by 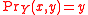 ) and X, Y are Fréchet space
) and X, Y are Fréchet space
s then strong duality holds.
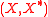 and
and  be dual pairs. Given a primal problem (minimize f(x)) and a related perturbation function (F(x,y)) then the Lagrangian
be dual pairs. Given a primal problem (minimize f(x)) and a related perturbation function (F(x,y)) then the Lagrangian  is the negative conjugate of F with respect to y (i.e. the concave conjugate). That is the Lagrangian is defined by
is the negative conjugate of F with respect to y (i.e. the concave conjugate). That is the Lagrangian is defined by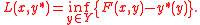
In particular the weak duality minmax equation can be shown to be
If the primal problem is given by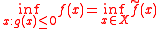
where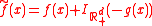 . Then if the perturbation is given by
. Then if the perturbation is given by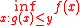
then the perturbation function is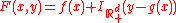 .
.
Thus the connection to Lagrangian duality can be seen, as L can be trivially seen to be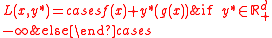 .
.
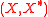 and
and 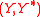 be dual pairs. Assume there exists a linear map
be dual pairs. Assume there exists a linear map 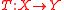 with adjoint operator
with adjoint operator 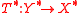 , and assume the primal objective function
, and assume the primal objective function  (including the constraints by way of the indicator function) can be written as
(including the constraints by way of the indicator function) can be written as 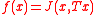 such that
such that 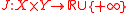 . Then the perturbation function is given by
. Then the perturbation function is given by
In particular if the primal objective is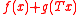 then the perturbation function is given by
then the perturbation function is given by  , which is the traditional definition of Fenchel duality.
, which is the traditional definition of Fenchel duality.
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
which relates to primal and dual problem
Dual problem
In constrained optimization, it is often possible to convert the primal problem to a dual form, which is termed a dual problem. Usually dual problem refers to the Lagrangian dual problem but other dual problems are used, for example, the Wolfe dual problem and the Fenchel dual problem...
s. The name comes from the fact that any such function defines a perturbation of the initial problem. In many cases this takes the form of shifting the constraints.
In some texts the value function is called the perturbation function, and the perturbation function is called the bifunction.
Definition
Given two dual pairDual pair
In functional analysis and related areas of mathematics a dual pair or dual system is a pair of vector spaces with an associated bilinear form....
s separated locally convex spaces
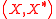 and
and  . Then given the function
. Then given the function 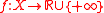 , we can define the primal problem by
, we can define the primal problem by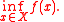
If there are constraint conditions, these can be built in to the function
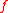 by letting
by letting  where
where 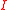 is the indicator function
is the indicator functionCharacteristic function (convex analysis)
In the field of mathematics known as convex analysis, the characteristic function of a set is a convex function that indicates the membership of a given element in that set...
. Then
 is a perturbation function if and only if
is a perturbation function if and only if 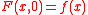 .
.Use in duality
The duality gapDuality gap
In optimization problems in applied mathematics, the duality gap is the difference between the primal and dual solutions. If d^* is the optimal dual value and p^* is the optimal primal value then the duality gap is equal to p^* - d^*. This value is always greater than or equal to 0. The duality...
is the difference of the right and left hand side of the inequality
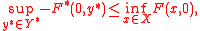
where
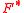 is the convex conjugate
is the convex conjugateConvex conjugate
In mathematics, convex conjugation is a generalization of the Legendre transformation. It is also known as Legendre–Fenchel transformation or Fenchel transformation .- Definition :...
in both variables.
For any choice of perturbation function F weak duality holds. There are a number of conditions which if satisfied imply strong duality. For instance, if F is proper
Proper convex function
In mathematical analysis and optimization, a proper convex function is a convex function f taking values in the extended real number line such thatf -\infty...
, jointly convex
Convex function
In mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...
, lower semi-continuous with
 (where
(where  is the algebraic interior
is the algebraic interiorAlgebraic interior
In functional analysis, a branch of mathematics, the algebraic interior or radial kernel of a subset of a vector space is a refinement of the concept of the interior. It is the subset of points contained in a given set that it is absorbing with respect to, i.e...
and
 is the projection onto Y defined by
is the projection onto Y defined by 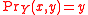 ) and X, Y are Fréchet space
) and X, Y are Fréchet spaceFréchet space
In functional analysis and related areas of mathematics, Fréchet spaces, named after Maurice Fréchet, are special topological vector spaces. They are generalizations of Banach spaces...
s then strong duality holds.
Lagrangian
Let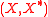 and
and  be dual pairs. Given a primal problem (minimize f(x)) and a related perturbation function (F(x,y)) then the Lagrangian
be dual pairs. Given a primal problem (minimize f(x)) and a related perturbation function (F(x,y)) then the Lagrangian  is the negative conjugate of F with respect to y (i.e. the concave conjugate). That is the Lagrangian is defined by
is the negative conjugate of F with respect to y (i.e. the concave conjugate). That is the Lagrangian is defined by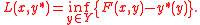
In particular the weak duality minmax equation can be shown to be

If the primal problem is given by
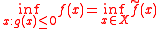
where
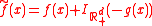 . Then if the perturbation is given by
. Then if the perturbation is given by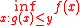
then the perturbation function is
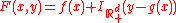 .
.Thus the connection to Lagrangian duality can be seen, as L can be trivially seen to be
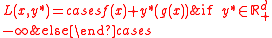 .
.Fenchel duality
Let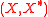 and
and 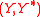 be dual pairs. Assume there exists a linear map
be dual pairs. Assume there exists a linear map 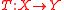 with adjoint operator
with adjoint operator 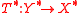 , and assume the primal objective function
, and assume the primal objective function  (including the constraints by way of the indicator function) can be written as
(including the constraints by way of the indicator function) can be written as 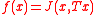 such that
such that 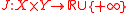 . Then the perturbation function is given by
. Then the perturbation function is given by
-
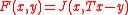 .
.
In particular if the primal objective is
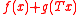 then the perturbation function is given by
then the perturbation function is given by  , which is the traditional definition of Fenchel duality.
, which is the traditional definition of Fenchel duality.

