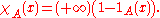Characteristic function (convex analysis)
Encyclopedia
In the field of mathematics
known as convex analysis
, the characteristic function of a set is a convex function
that indicates the membership (or non-membership) of a given element in that set. It is similar to the usual indicator function, and one can freely convert between the two, but the characteristic function as defined below is better-suited to the methods of convex analysis.
be a set, and let 
be a subset
of
. The characteristic function of 
is the function
taking values in the extended real number line
defined by
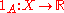denote the usual indicator function:
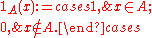
If one adopts the conventions that
then the indicator and characteristic functions are related by the equations
and
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
known as convex analysis
Convex analysis
Convex analysis is the branch of mathematics devoted to the study of properties of convex functions and convex sets, often with applications in convex minimization, a subdomain of optimization theory....
, the characteristic function of a set is a convex function
Convex function
In mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...
that indicates the membership (or non-membership) of a given element in that set. It is similar to the usual indicator function, and one can freely convert between the two, but the characteristic function as defined below is better-suited to the methods of convex analysis.
Definition
Let be a set, and let be a subsetSubset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of
. The characteristic function of is the functiontaking values in the extended real number line
Extended real number line
In mathematics, the affinely extended real number system is obtained from the real number system R by adding two elements: +∞ and −∞ . The projective extended real number system adds a single object, ∞ and makes no distinction between "positive" or "negative" infinity...
defined by
Relationship with the indicator function
Let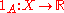 denote the usual indicator function: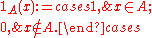If one adopts the conventions that
- for any
, 
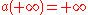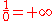and 
; -
; and -
;
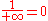then the indicator and characteristic functions are related by the equations
and