Oscillator Toda
Encyclopedia
In physics
, the Toda oscillator is special kind of nonlinear oscillator; it is vulgarization of the Toda field theory
, which is a continuous limit of Toda's chain, of chain of particles, with exponential potential of interaction between neighbors. These concepts are named afterMorikazu Toda. The Toda oscillator is used as simple model to understand the phenomenon of self-pulsation
, which is quasi-periodic pulsation of the output intensity of a solid-state laser
in the transient regime.
of any origin, which can be described with dependent coordinate
and independent coordinate 
, characterized in that the evolution
along independent coordinate
can be approximated with equation
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, the Toda oscillator is special kind of nonlinear oscillator; it is vulgarization of the Toda field theory
Toda field theory
In the study of field theory and partial differential equations, a Toda field theory is derived from the following Lagrangian:...
, which is a continuous limit of Toda's chain, of chain of particles, with exponential potential of interaction between neighbors. These concepts are named afterMorikazu Toda. The Toda oscillator is used as simple model to understand the phenomenon of self-pulsation
Self-pulsation
Self-pulsation takes place at the beginning of laser action.As the pump is switched on, the gainin the active medium rises and exceeds the steady-state value...
, which is quasi-periodic pulsation of the output intensity of a solid-state laser
Solid-state laser
A solid-state laser is a laser that uses a gain medium that is a solid, rather than a liquid such as in dye lasers or a gas as in gas lasers. Semiconductor-based lasers are also in the solid state, but are generally considered as a separate class from solid-state lasers .-Solid-state...
in the transient regime.
Definition
The Toda oscillator is a dynamical systemDynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
of any origin, which can be described with dependent coordinate
and independent coordinate , characterized in that the evolutionEvolution
Evolution is any change across successive generations in the heritable characteristics of biological populations. Evolutionary processes give rise to diversity at every level of biological organisation, including species, individual organisms and molecules such as DNA and proteins.Life on Earth...
along independent coordinate
can be approximated with equation
-
where
, 
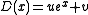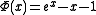and prime denotes the derivative.
Physical meaning
The independent coordinate
has sense of timeTimeTime is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....
. Indeed, it may be proportional to time
with some
relation like
, where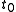 
is constant.
The derivativeDerivativeIn calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
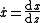may have sense of velocityVelocityIn physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
of particle with coordinate
; then 
can be interpreted as accelerationAccelerationIn physics, acceleration is the rate of change of velocity with time. In one dimension, acceleration is the rate at which something speeds up or slows down. However, since velocity is a vector, acceleration describes the rate of change of both the magnitude and the direction of velocity. ...
; and the mass of such a particle is equal to unity.
The dissipative function
may have sense of coefficient of the speed-proportional frictionFrictionFriction is the force resisting the relative motion of solid surfaces, fluid layers, and/or material elements sliding against each other. There are several types of friction:...
.
Usually, both parameters
and 
are supposed to be positive; then this speed-proportional friction coefficient grows exponentially at large positive values of coordinate 
.
The potential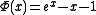
is fixed function, which also shows exponential grow at large positive values of coordinate 
.
In the application in laser physicsLaser PhysicsLaser Physics is an international scientific journal published by Nauka/Interperiodica. It is distributed through the Springer.-Topics covered:The journal specializes in laser physics, but also publishes papers about:...
,
may have sense of logarithmLogarithmThe logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
of number of photons in the laser cavity, related to its steady-state value. Then, the output power of such laser is proportional to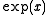
and may show pulsation at oscillationOscillationOscillation is the repetitive variation, typically in time, of some measure about a central value or between two or more different states. Familiar examples include a swinging pendulum and AC power. The term vibration is sometimes used more narrowly to mean a mechanical oscillation but sometimes...
of
.
Both analogies, with a unity mass particle and logarithm of number of photons are useful in the analysis of behavior of the Toda oscillator.
Energy
Rigorously, the oscillation is periodic only at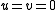
. Indeed in the realization of the Toda oscillator as a self-pulsing laser,
these parameters may have values of order of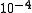
; during several pulses, the amplutude of pulsation does not change much. In this case, we can speak about period of pulsation, function 
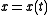is almost periodic.
In the case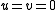
, the energy of oscillator 
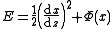does not depend on 
, and can be treated as constant of motion. Then, during one period of pulsation, the relation between 
and 
can be expressed analytically
,
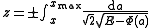
wehere
and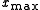 
are minimal and maximal values of 
; this solution is written for the case when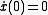 
.
however, other solutions may be obtained using the translational invariance.
The ratio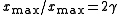
is convenient parameter to characterize the amplitude of pulsation,
then, the median value
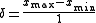
can be expressed as
;
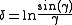and the energy
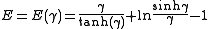
also is elementary function of
.
For the case
, an example of pulsation of the Toda oscillator is shown in Fig. 1.
In application, the quantity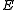
have no need to be physical energy of the system; in these cases, this dimension-less quantity may be called quasienergy.
Period of pulsation
The period of pulsation is increasing function of the amplitude
.
At
,
the period
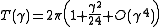
At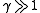
, the period
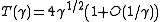
In the whole range
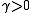, the period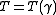 
and the frequency
can be approximated with
-
-
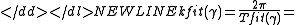
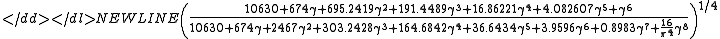
with at least 8 significant figures. The relative error of this approximation does not exceed
.
Decay of pulsation
At small (but still positive) values of
and 
, the pulsation decays slowly, and this decay can be described analytically. In the first approximation parameters 
and 
give additive contributions to the decay; the decay rate, as well as the amplitude and phase of the nonlinear oscillation can be approximated with elementary functions in the similar manner, as the period above. This allows to approximate the solution of the initial equation; and the error of such approximation is small compared to the difference between behavior of the idealized Toda oscillator and behavior of the experimental realization of the Toda oscillator as self-pulsing laser at the optical bench, although, qualitatively, a self-pulsing laser shows very similar behavior.
-
-