Ore condition
Encyclopedia
In mathematics
, especially in the area of algebra
known as ring theory
, the Ore condition is a condition introduced by Øystein Ore
, in connection with the question of extending beyond commutative ring
s the construction of a field of fractions
, or more generally localization of a ring
. The right Ore condition for a domain
R, and any pair a, b of non-zero elements, is the requirement that the sets aR and bR should intersect in more than the element 0. The left Ore condition is defined similarly. A domain that satisfies the right Ore condition is called a right Ore domain.
(a noncommutative field) with the same property. It turns out that the answer is sometimes "no", that is, there are domains which do not have an analogous "right division ring of fractions".
For every right Ore domain R, there is a unique (up to natural R-isomorphism) division ring D containing R as a subring such that every element of D is of the form rs−1 for r in R and s nonzero in R. Such a division ring D is called a ring of right fractions of R, and R is called a right order in D. The notion of a ring of left fractions and left order are defined analogously, with elements of D being of the form s−1r.
It is important to remember that the definition of R being a right order in D includes the condition that D must consist entirely of elements of the form rs−1. Any domain satisfying one of the Ore conditions can be considered a subring of a division ring, however this does not automatically mean R is a left order in D, since it is possible D has an element which is not of the form s−1r. Thus it is possible for R to be a right-not-left Ore domain. Intuitively, the condition that all elements of D be of the form rs−1 says that R is a "big" R-submodule of D. In fact the condition ensures RR is an essential submodule of DR. Lastly, there is even an example of a domain in a division ring which satisfies neither Ore condition (see examples below).
Another natural question is: "When is a subring of a division ring right Ore?" One characterization is that a subring R of a division ring D is a right Ore domain if and only if D is a flat
left R-module .
A different, stronger version of the Ore conditions is usually given for the case where R is not a domain, namely that there should be a common multiple
with u, v not zero divisor
s. In this case, Ore's theorem guarantees the existence of an over-ring called the (right or left) classical ring of quotients.
domains, such as right principal ideal domain
s, are also known to be right Ore domains. Even more generally, Alfred Goldie
proved that a domain R is right Ore if and only if RR has finite uniform dimension. It is also true that right Bézout domain
s are right Ore.
A subdomain of a division ring which is not right or left Ore: If F is any field, and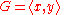
is the free monoid on two symbols x and y, then the monoid ring 
does not satisfy any Ore condition, but it is a free ideal ring
and thus indeed a subring of a division ring, by .
If S is a right denominator set, then one can construct the ring of right fractions RS−1 similarly to the commutative case. If S is taken to be the set of regular elements (those elements a in R such that if b in R is nonzero, then ab and ba are nonzero), then the right Ore condition is simply the requirement that S be a right denominator set.
Many properties of commutative localization hold in this more general setting. If S is a right denominator set for a ring R, then the left R-module RS−1 is flat
. Furthermore, if M is a right R-module, then the S-torsion, torS(M) = { m in M : ms = 0 for some s in S }, is an R-submodule isomorphic to Tor1(M,RS−1), and the module M ⊗R RS−1 is naturally isomorphic to a module MS−1 consisting of "fractions" as in the commutative case.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, especially in the area of algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
known as ring theory
Ring theory
In abstract algebra, ring theory is the study of rings—algebraic structures in which addition and multiplication are defined and have similar properties to those familiar from the integers...
, the Ore condition is a condition introduced by Øystein Ore
Øystein Ore
Øystein Ore was a Norwegian mathematician.-Life:Ore was graduated from the University of Oslo in 1922, with a Cand.Scient. degree in mathematics. In 1924, the University of Oslo awarded him the Ph.D. for a thesis titled Zur Theorie der algebraischen Körper, supervised by Thoralf Skolem...
, in connection with the question of extending beyond commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
s the construction of a field of fractions
Field of fractions
In abstract algebra, the field of fractions or field of quotients of an integral domain is the smallest field in which it can be embedded. The elements of the field of fractions of the integral domain R have the form a/b with a and b in R and b ≠ 0...
, or more generally localization of a ring
Localization of a ring
In abstract algebra, localization is a systematic method of adding multiplicative inverses to a ring. Given a ring R and a subset S, one wants to construct some ring R* and ring homomorphism from R to R*, such that the image of S consists of units in R*...
. The right Ore condition for a domain
Domain (ring theory)
In mathematics, especially in the area of abstract algebra known as ring theory, a domain is a ring such that ab = 0 implies that either a = 0 or b = 0. That is, it is a ring which has no left or right zero divisors. Some authors require the ring to be nontrivial...
R, and any pair a, b of non-zero elements, is the requirement that the sets aR and bR should intersect in more than the element 0. The left Ore condition is defined similarly. A domain that satisfies the right Ore condition is called a right Ore domain.
Application
Since it is well known that each integral domain is a subring of a field of fractions (via an embedding) in such a way that every element is of the form rs−1 with s nonzero, it is natural to ask if the same construction can take a noncommutative domain and associate a division ringDivision ring
In abstract algebra, a division ring, also called a skew field, is a ring in which division is possible. Specifically, it is a non-trivial ring in which every non-zero element a has a multiplicative inverse, i.e., an element x with...
(a noncommutative field) with the same property. It turns out that the answer is sometimes "no", that is, there are domains which do not have an analogous "right division ring of fractions".
For every right Ore domain R, there is a unique (up to natural R-isomorphism) division ring D containing R as a subring such that every element of D is of the form rs−1 for r in R and s nonzero in R. Such a division ring D is called a ring of right fractions of R, and R is called a right order in D. The notion of a ring of left fractions and left order are defined analogously, with elements of D being of the form s−1r.
It is important to remember that the definition of R being a right order in D includes the condition that D must consist entirely of elements of the form rs−1. Any domain satisfying one of the Ore conditions can be considered a subring of a division ring, however this does not automatically mean R is a left order in D, since it is possible D has an element which is not of the form s−1r. Thus it is possible for R to be a right-not-left Ore domain. Intuitively, the condition that all elements of D be of the form rs−1 says that R is a "big" R-submodule of D. In fact the condition ensures RR is an essential submodule of DR. Lastly, there is even an example of a domain in a division ring which satisfies neither Ore condition (see examples below).
Another natural question is: "When is a subring of a division ring right Ore?" One characterization is that a subring R of a division ring D is a right Ore domain if and only if D is a flat
Flat module
In Homological algebra, and algebraic geometry, a flat module over a ring R is an R-module M such that taking the tensor product over R with M preserves exact sequences. A module is faithfully flat if taking the tensor product with a sequence produces an exact sequence if and only if the original...
left R-module .
A different, stronger version of the Ore conditions is usually given for the case where R is not a domain, namely that there should be a common multiple
- c = au = bv
with u, v not zero divisor
Zero divisor
In abstract algebra, a nonzero element a of a ring is a left zero divisor if there exists a nonzero b such that ab = 0. Similarly, a nonzero element a of a ring is a right zero divisor if there exists a nonzero c such that ca = 0. An element that is both a left and a right zero divisor is simply...
s. In this case, Ore's theorem guarantees the existence of an over-ring called the (right or left) classical ring of quotients.
Examples
Commutative domains are automatically Ore domains, since for nonzero a and b, ab is nonzero in aR∩bR. Right NoetherianNoetherian
In mathematics, the adjective Noetherian is used to describe objects that satisfy an ascending or descending chain condition on certain kinds of subobjects; in particular,* Noetherian group, a group that satisfies the ascending chain condition on subgroups...
domains, such as right principal ideal domain
Principal ideal domain
In abstract algebra, a principal ideal domain, or PID, is an integral domain in which every ideal is principal, i.e., can be generated by a single element. More generally, a principal ideal ring is a nonzero commutative ring whose ideals are principal, although some authors refer to PIDs as...
s, are also known to be right Ore domains. Even more generally, Alfred Goldie
Alfred Goldie
Alfred William Goldie was an English mathematician.Goldie was Assistant Lecturer, Nottingham University 1946-48; Lecturer, then Senior Lecturer, Newcastle University 1948-63; and Professor of Pure Mathematics, Leeds University 1963-86;He won the 1970 Senior Berwick Prize from the London...
proved that a domain R is right Ore if and only if RR has finite uniform dimension. It is also true that right Bézout domain
Bézout domain
In mathematics, a Bézout domain is an integral domain in which the sum of two principal ideals is again a principal ideal. This means that for every pair of elements a Bézout identity holds, and that every finitely generated ideal is principal...
s are right Ore.
A subdomain of a division ring which is not right or left Ore: If F is any field, and
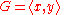is the free monoid on two symbols x and y, then the monoid ring does not satisfy any Ore condition, but it is a free ideal ringFree ideal ring
In mathematics, especially in the field of ring theory, a free ideal ring, or fir, is a ring in which all left ideals are free of unique rank. A ring such that all left ideals with at most n generators is free of unique rank is called an n-fir. A semifir is a ring in which all finitely generated...
and thus indeed a subring of a division ring, by .
Multiplicative sets
The Ore condition can be generalized to other multiplicative subsets, and is presented in textbook form in and . A subset S of a ring R is called a right denominator set if it satisfies the following three conditions for every a,b in R, and s, t in S:- st in S; (The set S is multiplicatively closed.)
- aS ∩ sR is not empty; (The set S is right permutable.)
- If sa = 0, then there is some u in S with au = 0; (The set S is right reversible.)
If S is a right denominator set, then one can construct the ring of right fractions RS−1 similarly to the commutative case. If S is taken to be the set of regular elements (those elements a in R such that if b in R is nonzero, then ab and ba are nonzero), then the right Ore condition is simply the requirement that S be a right denominator set.
Many properties of commutative localization hold in this more general setting. If S is a right denominator set for a ring R, then the left R-module RS−1 is flat
Flat module
In Homological algebra, and algebraic geometry, a flat module over a ring R is an R-module M such that taking the tensor product over R with M preserves exact sequences. A module is faithfully flat if taking the tensor product with a sequence produces an exact sequence if and only if the original...
. Furthermore, if M is a right R-module, then the S-torsion, torS(M) = { m in M : ms = 0 for some s in S }, is an R-submodule isomorphic to Tor1(M,RS−1), and the module M ⊗R RS−1 is naturally isomorphic to a module MS−1 consisting of "fractions" as in the commutative case.