Ordinal definable set
Encyclopedia
In mathematical set theory
, a set S is said to be ordinal definable if, informally, it can be defined in terms of a finite number of ordinals
by a first order formula. Ordinal definable sets were introduced by .
A drawback to this informal definition is that requires quantification over all first order formulas, which cannot be formalized in the language of set theory. However there is a different way of stating the definition which can be so formalized. In this approach, a set S is formally defined to be ordinal definable if there is some collection of ordinals α1...αn such that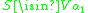
and 
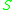can be defined as an element of 
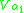by a first-order formula φ taking α2...αn as parameters. Here 
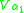denotes the set indexed by the ordinal α1 in the von Neumann hierarchy of sets
. In other words, S is the unique object such that φ(S, α2...αn) holds with its quantifiers ranging over
.
The class of all ordinal definable sets is denoted OD; it is not necessarily transitive
, and need not be a model of ZFC because it might not satisfy the axiom of extensionality
. A set is hereditarily ordinal definable if it is ordinal definable and all elements of its transitive closure
are ordinal definable. The class of hereditarily ordinal definable sets is denoted by HOD, and is a transitive model of ZFC, with a definable well ordering. It is consistent with the axioms of set theory that all sets are ordinal definable, and so hereditarily ordinal definable. The assertion that this situation holds is referred to as V = OD or V = HOD. It follows from V = L, and is equivalent to the existence of a (definable) well-ordering
of the universe. Note however that the formula expressing V = HOD need not hold true within HOD, as it is not absolute for models of set theory: within HOD, the interpretation of the formula for HOD may yield an even smaller inner model.
HOD has been found to be useful in that it is an inner model
that can accommodate essentially all known large cardinals. This is in contrast with the situation for core models
, as core models have not yet been constructed that can accommodate supercompact cardinals, for example.
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
, a set S is said to be ordinal definable if, informally, it can be defined in terms of a finite number of ordinals
Ordinal number
In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
by a first order formula. Ordinal definable sets were introduced by .
A drawback to this informal definition is that requires quantification over all first order formulas, which cannot be formalized in the language of set theory. However there is a different way of stating the definition which can be so formalized. In this approach, a set S is formally defined to be ordinal definable if there is some collection of ordinals α1...αn such that
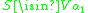and 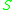can be defined as an element of 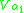by a first-order formula φ taking α2...αn as parameters. Here 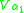denotes the set indexed by the ordinal α1 in the von Neumann hierarchy of setsVon Neumann universe
In set theory and related branches of mathematics, the von Neumann universe, or von Neumann hierarchy of sets, denoted V, is the class of hereditary well-founded sets...
. In other words, S is the unique object such that φ(S, α2...αn) holds with its quantifiers ranging over
.The class of all ordinal definable sets is denoted OD; it is not necessarily transitive
Transitive set
In set theory, a set A is transitive, if* whenever x ∈ A, and y ∈ x, then y ∈ A, or, equivalently,* whenever x ∈ A, and x is not an urelement, then x is a subset of A....
, and need not be a model of ZFC because it might not satisfy the axiom of extensionality
Axiom of extensionality
In axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of extensionality, or axiom of extension, is one of the axioms of Zermelo-Fraenkel set theory.- Formal statement :...
. A set is hereditarily ordinal definable if it is ordinal definable and all elements of its transitive closure
Transitive set
In set theory, a set A is transitive, if* whenever x ∈ A, and y ∈ x, then y ∈ A, or, equivalently,* whenever x ∈ A, and x is not an urelement, then x is a subset of A....
are ordinal definable. The class of hereditarily ordinal definable sets is denoted by HOD, and is a transitive model of ZFC, with a definable well ordering. It is consistent with the axioms of set theory that all sets are ordinal definable, and so hereditarily ordinal definable. The assertion that this situation holds is referred to as V = OD or V = HOD. It follows from V = L, and is equivalent to the existence of a (definable) well-ordering
Well-order
In mathematics, a well-order relation on a set S is a strict total order on S with the property that every non-empty subset of S has a least element in this ordering. Equivalently, a well-ordering is a well-founded strict total order...
of the universe. Note however that the formula expressing V = HOD need not hold true within HOD, as it is not absolute for models of set theory: within HOD, the interpretation of the formula for HOD may yield an even smaller inner model.
HOD has been found to be useful in that it is an inner model
Inner model
In mathematical logic, suppose T is a theory in the languageL = \langle \in \rangleof set theory.If M is a model of L describing a set theory and N is a class of M such that \langle N, \in_M, \ldots \rangle...
that can accommodate essentially all known large cardinals. This is in contrast with the situation for core models
Core model
In set theory, the core model is a definable inner model of the universe of all sets. Even though set theorists refer to "the core model", it is not a uniquely identified mathematical object. Rather, it is a class of inner models that under the right set theoretic assumptions have very special...
, as core models have not yet been constructed that can accommodate supercompact cardinals, for example.