
Numbering (computability theory)
Encyclopedia
In computability theory
a numbering is the assignment of natural number
s to a set of objects like rational number
s, graph
s or words in some language
. A numbering can be used to transfer the idea of computability and related concepts, which are strictly defined on the natural numbers using computable function
s, to different objects.
Important numberings are the Gödel numbering of the terms in first-order predicate calculus and numberings of the set of computable functions which can be used to apply results of computability theory on the set of computable functions itself.
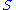 is a partial
is a partial
surjective function
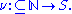
The value of at
at 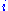 (if defined) is often written
(if defined) is often written  instead of the usual
instead of the usual 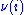 .
.  is called a total numbering if
is called a total numbering if  is a total function.
is a total function.
If is a set of natural numbers, then
is a set of natural numbers, then  is required to be a partial recursive function. If
is required to be a partial recursive function. If 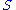 is a set of subsets of the natural numbers, then the set
is a set of subsets of the natural numbers, then the set  (using the Cantor pairing function) is required to be recursively enumerable.
(using the Cantor pairing function) is required to be recursively enumerable.

and
we say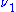 is reducible to
is reducible to  and write
and write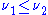
if
If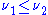 and
and  then we say
then we say 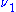 is equivalent to
is equivalent to  and write
and write  .
.
Computability theory
Computability theory, also called recursion theory, is a branch of mathematical logic that originated in the 1930s with the study of computable functions and Turing degrees. The field has grown to include the study of generalized computability and definability...
a numbering is the assignment of natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s to a set of objects like rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s, graph
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
s or words in some language
Language
Language may refer either to the specifically human capacity for acquiring and using complex systems of communication, or to a specific instance of such a system of complex communication...
. A numbering can be used to transfer the idea of computability and related concepts, which are strictly defined on the natural numbers using computable function
Computable function
Computable functions are the basic objects of study in computability theory. Computable functions are the formalized analogue of the intuitive notion of algorithm. They are used to discuss computability without referring to any concrete model of computation such as Turing machines or register...
s, to different objects.
Important numberings are the Gödel numbering of the terms in first-order predicate calculus and numberings of the set of computable functions which can be used to apply results of computability theory on the set of computable functions itself.
Definition
A numbering of a set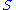 is a partial
is a partialPartial function
In mathematics, a partial function from X to Y is a function ƒ: X' → Y, where X' is a subset of X. It generalizes the concept of a function by not forcing f to map every element of X to an element of Y . If X' = X, then ƒ is called a total function and is equivalent to a function...
surjective function
Surjective function
In mathematics, a function f from a set X to a set Y is surjective , or a surjection, if every element y in Y has a corresponding element x in X so that f = y...
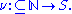
The value of
 at
at 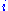 (if defined) is often written
(if defined) is often written  instead of the usual
instead of the usual 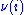 .
.  is called a total numbering if
is called a total numbering if  is a total function.
is a total function.If
 is a set of natural numbers, then
is a set of natural numbers, then  is required to be a partial recursive function. If
is required to be a partial recursive function. If 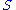 is a set of subsets of the natural numbers, then the set
is a set of subsets of the natural numbers, then the set  (using the Cantor pairing function) is required to be recursively enumerable.
(using the Cantor pairing function) is required to be recursively enumerable.Examples
- Given a Gödel numbering
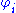 we can define a numbering of the recursively enumerable setRecursively enumerable setIn computability theory, traditionally called recursion theory, a set S of natural numbers is called recursively enumerable, computably enumerable, semidecidable, provable or Turing-recognizable if:...
we can define a numbering of the recursively enumerable setRecursively enumerable setIn computability theory, traditionally called recursion theory, a set S of natural numbers is called recursively enumerable, computably enumerable, semidecidable, provable or Turing-recognizable if:...
s by
Properties
It is often more convenient to work with a total numbering than with a partial one. If the domain of a partial numbering is recursively enumerable then there always exists an equivalent total numbering.Comparison of numberings
Using computable function we can define a partial ordering on the set of all numberings. Given two numberings
and

we say
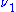 is reducible to
is reducible to  and write
and write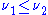
if

If
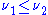 and
and  then we say
then we say 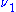 is equivalent to
is equivalent to  and write
and write  .
.

