Nonelementary integral
Encyclopedia
In mathematics
, a nonelementary antiderivative is an antiderivative
for which it can be shown that there exists no formula in terms of elementary functions (i.e. involving polynomials, and the standard functions sin, cos, exp, and so on). A theorem by Liouville
in 1835 provided the first proof that nonelementary antiderivatives exist. This theorem also provides a basis for determining (with difficulty) which expressions are integrable. It can be shown that, if one is given a function of any complexity, the probability that it will have an elementary antiderivative
are very low.
Some examples of such functions are:
The evaluation of nonelementary antiderivatives can often be done using Taylor series
. This is because Taylor series can always be integrated as one would an ordinary polynomial
, even if there is no elementary antiderivative of the function that generated the Taylor series.
However, in some cases it is not possible to rely on Taylor series. For example, if the function is not infinitely differentiable, one cannot generate a Taylor series. Even if a Taylor series can be generated, there is a good possibility that it will diverge
and not represent the function one is attempting to antidifferentiate. Many functions which are infinitely differentiable have higher order derivative
s that are unmanageable by hand. In these cases, it is not possible to evaluate indefinite integrals, but definite integrals can be evaluated numerically, for instance by Simpson's rule
. There are yet other cases where definite integrals can be evaluated exactly without numerical methods, but indefinite integrals cannot, for lack of an elementary antiderivative.
The integrals for many of these functions can be written down if one allows so-called "special" (nonelementary) functions. For example, the first example's integral is expressible using incomplete elliptic integrals of the first kind, the second and third use the logarithmic integral, the fourth the exponential integral
, and the fifth the error function
. Still, there exist functions, such as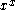
and 
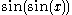for which no notation currently exists to describe their integrals (other than the use of the integrals themselves).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a nonelementary antiderivative is an antiderivative
Antiderivative
In calculus, an "anti-derivative", antiderivative, primitive integral or indefinite integralof a function f is a function F whose derivative is equal to f, i.e., F ′ = f...
for which it can be shown that there exists no formula in terms of elementary functions (i.e. involving polynomials, and the standard functions sin, cos, exp, and so on). A theorem by Liouville
Liouville's theorem (differential algebra)
In mathematics, Liouville's theorem, originally formulated by Joseph Liouville in the 1830s and 1840s, places an important restriction on antiderivatives that can be expressed as elementary functions....
in 1835 provided the first proof that nonelementary antiderivatives exist. This theorem also provides a basis for determining (with difficulty) which expressions are integrable. It can be shown that, if one is given a function of any complexity, the probability that it will have an elementary antiderivative
Antiderivative
In calculus, an "anti-derivative", antiderivative, primitive integral or indefinite integralof a function f is a function F whose derivative is equal to f, i.e., F ′ = f...
are very low.
Some examples of such functions are:
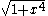
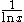
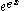
(see Normal distribution)
The evaluation of nonelementary antiderivatives can often be done using Taylor series
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
. This is because Taylor series can always be integrated as one would an ordinary polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
, even if there is no elementary antiderivative of the function that generated the Taylor series.
However, in some cases it is not possible to rely on Taylor series. For example, if the function is not infinitely differentiable, one cannot generate a Taylor series. Even if a Taylor series can be generated, there is a good possibility that it will diverge
Divergent series
In mathematics, a divergent series is an infinite series that is not convergent, meaning that the infinite sequence of the partial sums of the series does not have a limit....
and not represent the function one is attempting to antidifferentiate. Many functions which are infinitely differentiable have higher order derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
s that are unmanageable by hand. In these cases, it is not possible to evaluate indefinite integrals, but definite integrals can be evaluated numerically, for instance by Simpson's rule
Simpson's rule
In numerical analysis, Simpson's rule is a method for numerical integration, the numerical approximation of definite integrals. Specifically, it is the following approximation:...
. There are yet other cases where definite integrals can be evaluated exactly without numerical methods, but indefinite integrals cannot, for lack of an elementary antiderivative.
The integrals for many of these functions can be written down if one allows so-called "special" (nonelementary) functions. For example, the first example's integral is expressible using incomplete elliptic integrals of the first kind, the second and third use the logarithmic integral, the fourth the exponential integral
Exponential integral
In mathematics, the exponential integral is a special function defined on the complex plane given the symbol Ei.-Definitions:For real, nonzero values of x, the exponential integral Ei can be defined as...
, and the fifth the error function
Error function
In mathematics, the error function is a special function of sigmoid shape which occurs in probability, statistics and partial differential equations...
. Still, there exist functions, such as
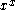and 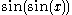for which no notation currently exists to describe their integrals (other than the use of the integrals themselves).See also
- list of integrals
- derivativeDerivativeIn calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
s - Risch algorithmRisch algorithmThe Risch algorithm, named after Robert Henry Risch, is an algorithm for the calculus operation of indefinite integration . The algorithm transforms the problem of integration into a problem in algebra. It is based on the form of the function being integrated and on methods for integrating rational...
- Symbolic integrationSymbolic integrationIn calculus symbolic integration is the problem of finding a formula for the antiderivative, or indefinite integral, of a given function f, i.e...