Noise temperature
Encyclopedia
In electronics, noise temperature is one way of expressing the level of available noise power introduced by a component or source. The power spectral density of the noise is expressed in terms of the temperature (in kelvins) that would produce that level of Johnson–Nyquist noise
, thus:
where:
Thus the noise temperature is proportional to the power spectral density of the noise,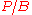
. That is the power that would be absorbed from the component or source by a matched load
. Noise temperature is generally a function of frequency, unlike that of an ideal resistor which is simply equal to the actual temperature of the resistor at all frequencies.
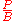, and would have a mean squared amplitude over a bandwidth B of:
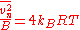
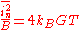
where R is the resistive part of the component's impedance
or G is the conductance (real part) of the component's admittance
. Speaking of noise temperature therefore offers a fair comparison between components having different impedances rather than specifying the noise voltage and qualifying that number by mentioning the component's resistance. It is also more accessible than speaking of the noise's power spectral density (in watts per hertz) since it is expressed as an ordinary temperature which can be compared to the noise level of an ideal resistor at room temperature (290 K).
Note that one can only speak of the noise temperature of a component or source whose impedance has a substantial (and measurable) resistive component. Thus it doesn't make sense to talk about the noise temperature of a capacitor or of a voltage source. The noise temperature of an amplifier
refers to the noise that would be added at the amplifier's input (relative to the input impedance of the amplifier) in order to account for the added noise observed following amplification.
, a communications channel
, and a receiver
. The communications channel may consist of a combination of different physical media, resulting in an electrical signal presented to the receiver. Whatever physical media a channel consists of, the transmitted signal will be attenuated and corrupted with additive noise
.
The additive noise in a receiving system can be of thermal origin (thermal noise) or can be from other noise-generating processes. Most noise processes will have a white
spectrum, at least over the bandwidth of interest, identical to that of thermal noise. Since they are indistinguishable, the contributions of all noise sources can be lumped together and regarded as a level of thermal noise. The noise power spectral density generated by all these sources (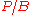
) can be described by assigning to the noise a temperature 
as defined above:
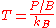
In a wireless communications receiver, the equivalent input noise temperature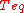
would equal the sum of two noise temperatures:
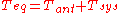
The antenna noise temperature
gives the noise power seen at the output of the antenna. The noise temperature of the receiver circuitry 
represents noise generated by noisy components inside the receiver.
Note that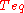
refers not to the noise at the output of the receiver after amplification, but the equivalent input noise power. In other words, the output of the receiver reflects that of a noiseless amplifier whose input had a noise level not of 
but of 
. Thus the figure of merit of a communications system is not the noise level at the speaker of a radio, for instance, since that depends on the setting of the receiver's gain. Rather we ask how much noise the receiver added to the original noise level, which is thus given by the factor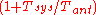 
. If a signal is present, then this factor represents the decrease in signal to noise ratio incurred using the receiver system with a noise temperature of 
.
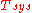or noise figure
. The noise factor specifies the increase in noise power (referred to the input of an amplifier) due to a component or system when its input noise temperature is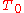
.
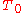is customarily taken to be room temperature, 290 K.
The noise factor (a linear term) is more often expressed as the noise figure (in decibels) using the conversion: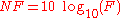
The noise figure can also be seen as the decrease in signal to noise ratio (SNR) caused by passing a signal through a system if the original signal had a noise temperature of 290 K. This is a common way of expressing the noise contributed by a radio frequency amplifier regardless of the amplifier's gain. For instance, assume an amplifier has a noise temperature 870 K and thus a noise figure of 6 dB. If that amplifier is used to amplify a source having a noise temperature of about room temperature (290 K), as many sources do, then the insertion of that amplifier would reduce the SNR of a signal by 6 dB. This simple relationship is frequently applicable where the source's noise is of thermal origin since a passive transducer will often have a noise temperature similar to 290 K.
However in many cases the input source's noise temperature is much higher, such as an antenna at lower frequencies where atmospheric noise dominates. Then there will be little degradation of the SNR. On the other hand a good satellite dish looking through the atmosphere into space (so that it sees a much lower noise temperature) would have the SNR of a signal degraded by more than 6 dB. In those cases a reference to the amplifier's noise temperature itself, rather than the noise figure defined according to room temperature, is more appropriate.
method. If there are multiple amplifiers in cascade, the noise temperature of the cascade can be calculated using the Friis equation:
where
Therefore the amplifier chain can be modelled as a black box
having a gain of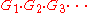
and a noise figure given by 
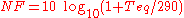. In the usual case where the gains of the amplifier's stages are much greater than one, then it can be seen that the noise temperatures of the earlier stages have a much greater influence on the resulting noise temperature than those later in the chain. One can appreciate that the noise introduced by the first stage, for instance, is amplified by all of the stages whereas the noise introduced by later stages undergoes lesser amplification. Another way of looking at it is that the signal applied to a later stage already has a high noise level, due to amplification of noise by the previous stages, so that the noise contribution of that stage to that already amplified signal is of less significance.
This explains why the quality of a preamplifier
or RF amplifier
is of particular importance in an amplifier chain. In most cases only the noise figure of the first stage need be considered. However one must check that the noise figure of the second stage is not so high (or that the gain of the first stage is so low) that there is SNR degradation due to the second stage anyway. That will be a concern if the noise figure of the first stage plus that stage's gain (in decibels) is not much greater than the noise figure of the second stage.
One corollary of the Friis equation is that an attenuator
prior to the first amplifier will degrade the noise figure due to the amplifier. For instance, if stage 1 represents a 6 dB attenuator so that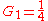
, then 
. Effectively the noise temperature of the amplifier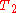 
has been quadrupled, in addition to the (smaller) contribution due to the attenuator itself 
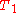(usually room temperature if the attenuator is composed of resistors). An antenna with poor efficiency
is an example of this principle, where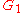
would represent the antenna's efficiency.
Johnson–Nyquist noise
Johnson–Nyquist noise is the electronic noise generated by the thermal agitation of the charge carriers inside an electrical conductor at equilibrium, which happens regardless of any applied voltage...
, thus:
where:
is the power (in watts)
is the total bandwidth (Hz) over which that noise power is measured
is the Boltzmann constant (1.381×10−23 J/K, joules per kelvin)
is the noise temperature (K)
Thus the noise temperature is proportional to the power spectral density of the noise,
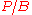. That is the power that would be absorbed from the component or source by a matched loadImpedance matching
In electronics, impedance matching is the practice of designing the input impedance of an electrical load to maximize the power transfer and/or minimize reflections from the load....
. Noise temperature is generally a function of frequency, unlike that of an ideal resistor which is simply equal to the actual temperature of the resistor at all frequencies.
Noise voltage and current
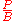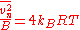
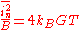
A noisy component may be modelled as a noiseless component in series with a noisy voltage source producing a voltage of vn, or as a noiseless component in parallel with a noisy current source producing a current of in. This equivalent voltage or current corresponds to the above power spectral density, and would have a mean squared amplitude over a bandwidth B of:where R is the resistive part of the component's impedance
Impedance
Impedance may refer to:*Electrical impedance, the ratio of the voltage phasor to the electric current phasor, a measure of the opposition to time-varying electric current in an electric circuit**Characteristic impedance of a transmission line...
or G is the conductance (real part) of the component's admittance
Admittance
In electrical engineering, the admittance is a measure of how easily a circuit or device will allow a current to flow. It is defined as the inverse of the impedance . The SI unit of admittance is the siemens...
. Speaking of noise temperature therefore offers a fair comparison between components having different impedances rather than specifying the noise voltage and qualifying that number by mentioning the component's resistance. It is also more accessible than speaking of the noise's power spectral density (in watts per hertz) since it is expressed as an ordinary temperature which can be compared to the noise level of an ideal resistor at room temperature (290 K).
Note that one can only speak of the noise temperature of a component or source whose impedance has a substantial (and measurable) resistive component. Thus it doesn't make sense to talk about the noise temperature of a capacitor or of a voltage source. The noise temperature of an amplifier
Amplifier
Generally, an amplifier or simply amp, is a device for increasing the power of a signal.In popular use, the term usually describes an electronic amplifier, in which the input "signal" is usually a voltage or a current. In audio applications, amplifiers drive the loudspeakers used in PA systems to...
refers to the noise that would be added at the amplifier's input (relative to the input impedance of the amplifier) in order to account for the added noise observed following amplification.
Application to communication systems
A communications system is typically made up of a transmitterTransmitter
In electronics and telecommunications a transmitter or radio transmitter is an electronic device which, with the aid of an antenna, produces radio waves. The transmitter itself generates a radio frequency alternating current, which is applied to the antenna. When excited by this alternating...
, a communications channel
Channel (communications)
In telecommunications and computer networking, a communication channel, or channel, refers either to a physical transmission medium such as a wire, or to a logical connection over a multiplexed medium such as a radio channel...
, and a receiver
Receiver (radio)
A radio receiver converts signals from a radio antenna to a usable form. It uses electronic filters to separate a wanted radio frequency signal from all other signals, the electronic amplifier increases the level suitable for further processing, and finally recovers the desired information through...
. The communications channel may consist of a combination of different physical media, resulting in an electrical signal presented to the receiver. Whatever physical media a channel consists of, the transmitted signal will be attenuated and corrupted with additive noise
Additive white Gaussian noise
Additive white Gaussian noise is a channel model in which the only impairment to communication is a linear addition of wideband or white noise with a constant spectral density and a Gaussian distribution of amplitude. The model does not account for fading, frequency selectivity, interference,...
.
The additive noise in a receiving system can be of thermal origin (thermal noise) or can be from other noise-generating processes. Most noise processes will have a white
White noise
White noise is a random signal with a flat power spectral density. In other words, the signal contains equal power within a fixed bandwidth at any center frequency...
spectrum, at least over the bandwidth of interest, identical to that of thermal noise. Since they are indistinguishable, the contributions of all noise sources can be lumped together and regarded as a level of thermal noise. The noise power spectral density generated by all these sources (
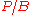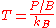
) can be described by assigning to the noise a temperature as defined above:In a wireless communications receiver, the equivalent input noise temperature
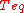would equal the sum of two noise temperatures: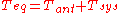The antenna noise temperature
gives the noise power seen at the output of the antenna. The noise temperature of the receiver circuitry represents noise generated by noisy components inside the receiver.Note that
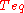refers not to the noise at the output of the receiver after amplification, but the equivalent input noise power. In other words, the output of the receiver reflects that of a noiseless amplifier whose input had a noise level not of but of . Thus the figure of merit of a communications system is not the noise level at the speaker of a radio, for instance, since that depends on the setting of the receiver's gain. Rather we ask how much noise the receiver added to the original noise level, which is thus given by the factor 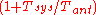. If a signal is present, then this factor represents the decrease in signal to noise ratio incurred using the receiver system with a noise temperature of 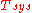.Noise figure
One use of noise temperature is in the definition of a system's noise factorNoise figure
Noise figure is a measure of degradation of the signal-to-noise ratio , caused by components in a radio frequency signal chain. The noise figure is defined as the ratio of the output noise power of a device to the portion thereof attributable to thermal noise in the input termination at standard...
or noise figure
Noise figure
Noise figure is a measure of degradation of the signal-to-noise ratio , caused by components in a radio frequency signal chain. The noise figure is defined as the ratio of the output noise power of a device to the portion thereof attributable to thermal noise in the input termination at standard...
. The noise factor specifies the increase in noise power (referred to the input of an amplifier) due to a component or system when its input noise temperature is
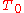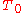. is customarily taken to be room temperature, 290 K.The noise factor (a linear term) is more often expressed as the noise figure (in decibels) using the conversion:
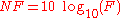
The noise figure can also be seen as the decrease in signal to noise ratio (SNR) caused by passing a signal through a system if the original signal had a noise temperature of 290 K. This is a common way of expressing the noise contributed by a radio frequency amplifier regardless of the amplifier's gain. For instance, assume an amplifier has a noise temperature 870 K and thus a noise figure of 6 dB. If that amplifier is used to amplify a source having a noise temperature of about room temperature (290 K), as many sources do, then the insertion of that amplifier would reduce the SNR of a signal by 6 dB. This simple relationship is frequently applicable where the source's noise is of thermal origin since a passive transducer will often have a noise temperature similar to 290 K.
However in many cases the input source's noise temperature is much higher, such as an antenna at lower frequencies where atmospheric noise dominates. Then there will be little degradation of the SNR. On the other hand a good satellite dish looking through the atmosphere into space (so that it sees a much lower noise temperature) would have the SNR of a signal degraded by more than 6 dB. In those cases a reference to the amplifier's noise temperature itself, rather than the noise figure defined according to room temperature, is more appropriate.
Noise temperature of an amplifier chain
The noise temperature of an amplifier is commonly measured using the Y-factorY-factor
The Y-factor method is a widely used technique for measuring the gain and noise temperature of an amplifier. It is based on the Johnson-Nyquist noise of a resistor at two different, known temperatures....
method. If there are multiple amplifiers in cascade, the noise temperature of the cascade can be calculated using the Friis equation:
where
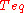= resulting noise temperature referred to the input
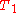= noise temperature of the first component in the cascade
= noise temperature of the second component in the cascade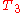
= noise temperature of the third component in the cascade
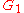= power gain of the first component in the cascade
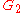= power gain of the second component in the cascade
Therefore the amplifier chain can be modelled as a black box
Black box
A black box is a device, object, or system whose inner workings are unknown; only the input, transfer, and output are known characteristics.The term black box can also refer to:-In science and technology:*Black box theory, a philosophical theory...
having a gain of
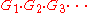and a noise figure given by 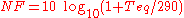. In the usual case where the gains of the amplifier's stages are much greater than one, then it can be seen that the noise temperatures of the earlier stages have a much greater influence on the resulting noise temperature than those later in the chain. One can appreciate that the noise introduced by the first stage, for instance, is amplified by all of the stages whereas the noise introduced by later stages undergoes lesser amplification. Another way of looking at it is that the signal applied to a later stage already has a high noise level, due to amplification of noise by the previous stages, so that the noise contribution of that stage to that already amplified signal is of less significance.This explains why the quality of a preamplifier
Preamplifier
A preamplifier is an electronic amplifier that prepares a small electrical signal for further amplification or processing. A preamplifier is often placed close to the sensor to reduce the effects of noise and interference. It is used to boost the signal strength to drive the cable to the main...
or RF amplifier
Low-noise amplifier
Low-noise amplifier is an electronic amplifier used to amplify possibly very weak signals . It is usually located very close to the detection device to reduce losses in the feedline. This active antenna arrangement is frequently used in microwave systems like GPS, because coaxial cable feedline is...
is of particular importance in an amplifier chain. In most cases only the noise figure of the first stage need be considered. However one must check that the noise figure of the second stage is not so high (or that the gain of the first stage is so low) that there is SNR degradation due to the second stage anyway. That will be a concern if the noise figure of the first stage plus that stage's gain (in decibels) is not much greater than the noise figure of the second stage.
One corollary of the Friis equation is that an attenuator
Attenuator (electronics)
An attenuator is an electronic device that reduces the amplitude or power of a signal without appreciably distorting its waveform.An attenuator is effectively the opposite of an amplifier, though the two work by different methods...
prior to the first amplifier will degrade the noise figure due to the amplifier. For instance, if stage 1 represents a 6 dB attenuator so that
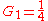, then . Effectively the noise temperature of the amplifier 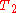has been quadrupled, in addition to the (smaller) contribution due to the attenuator itself 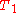(usually room temperature if the attenuator is composed of resistors). An antenna with poor efficiencyAntenna efficiency
In electromagnetics, antenna efficiency or radiation efficiency is a figure of merit for an antenna. It measures the electrical losses that occur throughout the antenna while it is operating at a given frequency, or averaged over its operation across a frequency band...
is an example of this principle, where
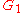would represent the antenna's efficiency.