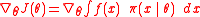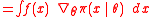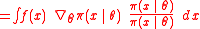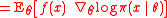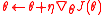Natural evolution strategy
Encyclopedia
Natural evolution strategies (NES) are a family of numerical optimization algorithms for black-box
problems. Similar in spirit to evolution strategies, they iteratively update the (continuous) parameters of a search distribution by following the natural gradient towards higher expected fitness.
is evaluated at each such point. The distribution’s parameters (which include strategy parameters) allow the algorithm to adaptively capture the (local) structure of the fitness function. For example, in the case of a Gaussian distribution, this comprises the mean and the covariance matrix
. From the samples, NES estimates a search gradient on the parameters towards higher expected fitness. NES then performs a gradient ascent step along the natural gradient, a second order method which, unlike the plain gradient, renormalizes the update w.r.t. uncertainty. This step is crucial, since it prevents oscillations, premature convergence, and undesired effects stemming from a given parameterization. The entire process reiterates until a stopping criterion is met.
All members of the NES family operate based on the same principles. They differ in the type of probability distribution
and the gradient approximation
method used. Different search spaces require different search distributions; for example, in low dimensionality it can be highly beneficial to model the full covariance matrix. In high dimensions, on the other hand, a more scalable alternative is to limit the covariance to the diagonal
only. In addition, highly multi-modal search spaces may benefit from more heavy-tailed distributions
(such as Cauchy
, as opposed to the Gaussian). A last distinction arises between distributions where we can analytically compute the natural gradient, and more general distributions where we need to estimate it from samples.
 denote the parameters of the search distribution
denote the parameters of the search distribution  and
and  the fitness function evaluated at
the fitness function evaluated at  . NES then pursues the objective of maximizing the expected fitness under the search distribution
. NES then pursues the objective of maximizing the expected fitness under the search distribution
through gradient ascent. The gradient can be rewritten as
that is, the expected value
of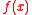 times the log-derivatives
times the log-derivatives
at . In practice, it is possible to use the Monte Carlo
. In practice, it is possible to use the Monte Carlo
approximation based on a finite number of samples
samples
Black box
A black box is a device, object, or system whose inner workings are unknown; only the input, transfer, and output are known characteristics.The term black box can also refer to:-In science and technology:*Black box theory, a philosophical theory...
problems. Similar in spirit to evolution strategies, they iteratively update the (continuous) parameters of a search distribution by following the natural gradient towards higher expected fitness.
Method
The general procedure is as follows: the parameterized search distribution is used to produce a batch of search points, and the fitness functionFitness function
A fitness function is a particular type of objective function that is used to summarise, as a single figure of merit, how close a given design solution is to achieving the set aims....
is evaluated at each such point. The distribution’s parameters (which include strategy parameters) allow the algorithm to adaptively capture the (local) structure of the fitness function. For example, in the case of a Gaussian distribution, this comprises the mean and the covariance matrix
Covariance matrix
In probability theory and statistics, a covariance matrix is a matrix whose element in the i, j position is the covariance between the i th and j th elements of a random vector...
. From the samples, NES estimates a search gradient on the parameters towards higher expected fitness. NES then performs a gradient ascent step along the natural gradient, a second order method which, unlike the plain gradient, renormalizes the update w.r.t. uncertainty. This step is crucial, since it prevents oscillations, premature convergence, and undesired effects stemming from a given parameterization. The entire process reiterates until a stopping criterion is met.
All members of the NES family operate based on the same principles. They differ in the type of probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
and the gradient approximation
Approximation
An approximation is a representation of something that is not exact, but still close enough to be useful. Although approximation is most often applied to numbers, it is also frequently applied to such things as mathematical functions, shapes, and physical laws.Approximations may be used because...
method used. Different search spaces require different search distributions; for example, in low dimensionality it can be highly beneficial to model the full covariance matrix. In high dimensions, on the other hand, a more scalable alternative is to limit the covariance to the diagonal
Diagonal matrix
In linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...
only. In addition, highly multi-modal search spaces may benefit from more heavy-tailed distributions
Heavy-tailed distribution
In probability theory, heavy-tailed distributions are probability distributions whose tails are not exponentially bounded: that is, they have heavier tails than the exponential distribution...
(such as Cauchy
Cauchy distribution
The Cauchy–Lorentz distribution, named after Augustin Cauchy and Hendrik Lorentz, is a continuous probability distribution. As a probability distribution, it is known as the Cauchy distribution, while among physicists, it is known as the Lorentz distribution, Lorentz function, or Breit–Wigner...
, as opposed to the Gaussian). A last distinction arises between distributions where we can analytically compute the natural gradient, and more general distributions where we need to estimate it from samples.
Search gradients
Let denote the parameters of the search distribution
denote the parameters of the search distribution  and
and  the fitness function evaluated at
the fitness function evaluated at  . NES then pursues the objective of maximizing the expected fitness under the search distribution
. NES then pursues the objective of maximizing the expected fitness under the search distribution
through gradient ascent. The gradient can be rewritten as
that is, the expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
of
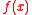 times the log-derivatives
times the log-derivativesLogarithmic derivative
In mathematics, specifically in calculus and complex analysis, the logarithmic derivative of a function f is defined by the formulawhere f ′ is the derivative of f....
at
 . In practice, it is possible to use the Monte Carlo
. In practice, it is possible to use the Monte CarloMonte Carlo method
Monte Carlo methods are a class of computational algorithms that rely on repeated random sampling to compute their results. Monte Carlo methods are often used in computer simulations of physical and mathematical systems...
approximation based on a finite number of
 samples
samples
-
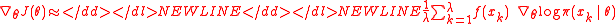 .
.
Finally, the parameters of the search distribution can be updated iteratively
Natural gradient ascent
Instead of using the plain stochastic gradient for updates, NES
follows the natural gradient, which has been shown to
possess numerous advantages over the plain (vanilla) gradient, e.g.:- the gradient direction is independent of the parameterization of the search distribution
- the updates magnitudes are automatically adjusted based on uncertainty, in turn speeding convergence on plateausPlateau (mathematics)A plateau of a function is a part of its domain where the function has constant value.More formally, let U, V be topological spaces. A plateau for a function f: U → V is a path-connected set of points P of U such that for some y we havefor all p in P....
and ridges.
The NES update is therefore-
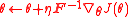 ,
,
where is the Fisher information matrix.
is the Fisher information matrix.
The Fisher matrix can sometimes be computed exactly, otherwise it is estimated from samples, reusing the log-derivatives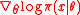 .
.
Fitness shaping
NES utilizes rankRankingA ranking is a relationship between a set of items such that, for any two items, the first is either 'ranked higher than', 'ranked lower than' or 'ranked equal to' the second....
-based fitness shaping in order to render the
algorithm more robust, and invariant under monotonically
increasing transformations of the fitness function.
For this purpose, the fitness of the population is transformed into a set of utilityUtilityIn economics, utility is a measure of customer satisfaction, referring to the total satisfaction received by a consumer from consuming a good or service....
values
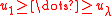 . Let
. Let 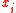 denote the ith best individual.
denote the ith best individual.
Replacing fitness with utility, the gradient estimate becomes-
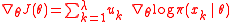 .
.
The choice of utility function is a free parameter of the algorithm.
Pseudocode
input: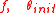
1 repeat
2 for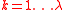 do //
do //  is the population size
is the population size
3 draw sample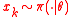
4 evaluate fitness
5 calculate log-derivatives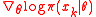
6 end
7 assign the utilities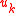 // based on rank
// based on rank
8 estimate the gradient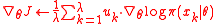
9 estimate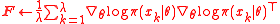 // or compute it exactly
// or compute it exactly
10 update parameters //
// 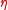 is the learning rate
is the learning rate
11 until stopping criterion is met
See also
- Evolutionary computationEvolutionary computationIn computer science, evolutionary computation is a subfield of artificial intelligence that involves combinatorial optimization problems....
- Covariance matrix adaptation evolution strategy (CMA-ES)CMA-ESCMA-ES stands for Covariance Matrix Adaptation Evolution Strategy. Evolution strategies are stochastic, derivative-free methods for numerical optimization of non-linear or non-convex continuous optimization problems. They belong to the class of evolutionary algorithms and evolutionary computation...
External links
-