In graph theory

Graph theory

In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...

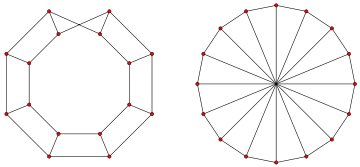
, the Möbius ladder M_n is a cubic

Cubic graph

In the mathematical field of graph theory, a cubic graph is a graph in which all vertices have degree three. In other words a cubic graph is a 3-regular graph. Cubic graphs are also called trivalent graphs....

 circulant graph

Circulant graph

In graph theory, a circulant graph is an undirected graph that has a cyclic group of symmetries that includes a symmetry taking any vertex to any other vertex.-Equivalent definitions:Circulant graphs can be described in several equivalent ways:...

 with an even number n of vertices, formed from an n-cycle

Cycle graph

In graph theory, a cycle graph or circular graph is a graph that consists of a single cycle, or in other words, some number of vertices connected in a closed chain. The cycle graph with n vertices is called Cn...

 by adding edges (called "rungs") connecting opposite pairs of vertices in the cycle. It is so-named because (with the exception of M₆ = K_3,3

Complete bipartite graph

In the mathematical field of graph theory, a complete bipartite graph or biclique is a special kind of bipartite graph where every vertex of the first set is connected to every vertex of the second set.- Definition :...

) M_n has exactly n/2 4-cycles (McSorley 1998) which link together by their shared edges to form a topological Möbius strip

Möbius strip

The Möbius strip or Möbius band is a surface with only one side and only one boundary component. The Möbius strip has the mathematical property of being non-orientable. It can be realized as a ruled surface...

. Möbius ladders were named and first studied by Guy

Richard K. Guy

Richard Kenneth Guy is a British mathematician, Professor Emeritus in the Department of Mathematics at the University of Calgary....

 and Harary

Frank Harary

Frank Harary was a prolific American mathematician, who specialized in graph theory. He was widely recognized as one of the "fathers" of modern graph theory....

 (1967).

Properties

Every Möbius ladder is a nonplanar

Planar graph

In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...

 apex graph

Apex graph

In graph theory, a branch of mathematics, an apex graph is a graph that can be made planar by the removal of a single vertex. The deleted vertex is called an apex of the graph. We say an apex, not the apex because an apex graph may have more than one apex...

. Möbius ladders have crossing number

Crossing number (graph theory)

In graph theory, the crossing number cr of a graph G is the lowest number of edge crossings of a planar drawing of the graph G. For instance, a graph is planar if and only if its crossing number is zero.The concept originated in...

 one, and can be embedded without crossings on a torus

Torus

In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...

 or projective plane

Projective plane

In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect...

. Thus, they are examples of toroidal graph

Toroidal graph

In mathematics, a graph G is toroidal if it can be embedded on the torus. In other words, the graph's vertices can be placed on a torus such that no edges cross...

s. Li (2005) explores embeddings of these graphs onto higher genus surfaces.

Möbius ladders are vertex-transitive

Vertex-transitive graph

In the mathematical field of graph theory, a vertex-transitive graph is a graph G such that, given any two vertices v1 and v2 of G, there is some automorphismf:V \rightarrow V\ such thatf = v_2.\...

 but (again with the exception of M₆) not edge-transitive: each edge from the cycle from which the ladder is formed belongs to a single 4-cycle, while each rung belongs to two such cycles.

When n ≡ 2 (mod 4), M_n is bipartite

Bipartite graph

In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V; that is, U and V are independent sets...

. When n ≡ 0 (mod 4), by Brooks' theorem M_n has chromatic number 3. De Mier and Noy (2005) show that the Möbius ladders are uniquely determined by their chromatic polynomial

Chromatic polynomial

The chromatic polynomial is a polynomial studied in algebraic graph theory, a branch of mathematics. It counts the number of graph colorings as a function of the number of colors and was originally defined by George David Birkhoff to attack the four color problem. It was generalised to the Tutte...

s.

The Möbius ladder M₈ has 392 spanning tree

Spanning tree

Spanning tree can refer to:* Spanning tree , a tree which contains every vertex of a more general graph* Spanning tree protocol, a protocol for finding spanning trees in bridged networks...

s; it and M₆ have the most spanning trees among all cubic graphs with the same number of vertices (Jakobson and Rivin 1999; Valdes 1991). However, the 10-vertex graph with the most spanning trees is the Petersen graph

Petersen graph

In the mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is named for Julius Petersen, who in 1898 constructed it...

, which is not a Möbius ladder.

Graph minors

Möbius ladders play an important role in the theory of graph minors

Minor (graph theory)

In graph theory, an undirected graph H is called a minor of the graph G if H is isomorphic to a graph that can be obtained by zero or more edge contractions on a subgraph of G....

. The earliest result of this type is a 1937 theorem of Klaus Wagner

Klaus Wagner (mathematician)

Klaus Wagner was a German mathematician. He studied topology at the University of Cologne under the supervision of Karl Dörge, who had been a student of Issai Schur. Wagner received his Ph.D. in 1937, and taught at Cologne for many years himself...

 that graphs with no K₅ minor can be formed by using clique-sum

Clique-sum

In graph theory, a branch of mathematics, a clique-sum is a way of combining two graphs by gluing them together at a clique, analogous to the connected sum operation in topology...

 operations to combine planar graphs and the Möbius ladder M₈; for this reason M₈ is called the Wagner graph

Wagner graph

In the mathematical field of graph theory, the Wagner graph is a 3-regular graph with 8 vertices and 12 edges. It is the 8-vertex Möbius ladder graph.-Properties:...

.

Gubser (1996) defines an almost-planar graph to be a nonplanar graph for which every nontrivial minor is planar; he shows that 3-connected almost-planar graphs are Möbius ladders or members of a small number of other families, and that other almost-planar graphs can be formed from these by a sequence of simple operations.

Maharry (2001) shows that almost all graphs that do not have a cube minor can be derived by a sequence of simple operations from Möbius ladders.

Chemistry and physics

Walba et al. (1982) first synthesized molecular structures in the form of a Möbius ladder, and since then this structure has been of interest in chemistry and chemical stereography (Simon 1993), especially in view of the ladder-like form of DNA molecules. With this application in mind, Flapan (1989) studies the mathematical symmetries of embeddings of Möbius ladders in R³.

Möbius ladders have also been used as the shape of a superconducting

Superconductivity

Superconductivity is a phenomenon of exactly zero electrical resistance occurring in certain materials below a characteristic temperature. It was discovered by Heike Kamerlingh Onnes on April 8, 1911 in Leiden. Like ferromagnetism and atomic spectral lines, superconductivity is a quantum...

 ring in experiments to study the effects of conductor topology on electron interactions (Mila et al. 1998; Deng et al. 2002).

Combinatorial optimization

Möbius ladders have also been used in computer science

Computer science

Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...

, as part of integer programming

Integer programming

An integer programming problem is a mathematical optimization or feasibility program in which some or all of the variables are restricted to be integers. In many settings the term refers to integer linear programming, which is also known as mixed integer programming.Integer programming is NP-hard...

 approaches to problems of set packing and linear ordering. Certain configurations within these problems can be used to define facets of the polytope

Polytope

In elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...

 describing a linear programming

Linear programming

Linear programming is a mathematical method for determining a way to achieve the best outcome in a given mathematical model for some list of requirements represented as linear relationships...

 relaxation of the problem; these facets are called Möbius ladder constraints (Bolotashvili et al. 1999; Borndörfer and Weismantel 2000; Grötschel et al. 1985a, 1985b; Newman and Vempala 2004).