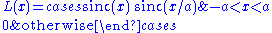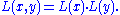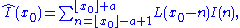Lanczos resampling
Encyclopedia

Multivariate interpolation
In numerical analysis, multivariate interpolation or spatial interpolation is interpolation on functions of more than one variable.The function to be interpolated is known at given points and the interpolation problem consist of yielding values at arbitrary points .-Regular grid:For function...
, for example for image scaling
Image scaling
In computer graphics, image scaling is the process of resizing a digital image. Scaling is a non-trivial process that involves a trade-off between efficiency, smoothness and sharpness. As the size of an image is increased, so the pixels which comprise the image become increasingly visible, making...
(to resize digital images), but can be used for any other digital signal. The Lanczos kernel indicates which samples in the original data, and in what proportion, make up each sample of the final data.
The filter is named after Cornelius Lanczos
Cornelius Lanczos
Cornelius Lanczos Löwy Kornél was a Hungarian-Jewish mathematician and physicist, who was born on February 2, 1893, and died on June 25, 1974....
,
because he showed how to use Fourier series
Fourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
and Chebyshev polynomials
Chebyshev polynomials
In mathematics the Chebyshev polynomials, named after Pafnuty Chebyshev, are a sequence of orthogonal polynomials which are related to de Moivre's formula and which can be defined recursively. One usually distinguishes between Chebyshev polynomials of the first kind which are denoted Tn and...
for various problems where they had not been used before.
Application
The Lanczos filter is a windowedWindow function
In signal processing, a window function is a mathematical function that is zero-valued outside of some chosen interval. For instance, a function that is constant inside the interval and zero elsewhere is called a rectangular window, which describes the shape of its graphical representation...
form of the sinc filter
Sinc filter
In signal processing, a sinc filter is an idealized filter that removes all frequency components above a given bandwidth, leaves the low frequencies alone, and has linear phase...
(a theoretically optimal "brick-wall" low-pass filter
Low-pass filter
A low-pass filter is an electronic filter that passes low-frequency signals but attenuates signals with frequencies higher than the cutoff frequency. The actual amount of attenuation for each frequency varies from filter to filter. It is sometimes called a high-cut filter, or treble cut filter...
). The sinc function is infinite in extent, and thus not directly usable in practice. Instead, one uses approximations, called windowed forms of the filter, as discussed in window functions: filter design, and the Lanczos filter is one such windowing. The windows vanish outside of a range, and using larger ranges allows one to improve accuracy in exchange for more computation.
Some have compared the Lanczos filter favorably with simpler filters or other windowings of sinc, finding it the "best compromise" among filters considered.
Definition
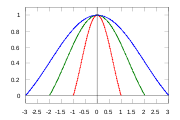
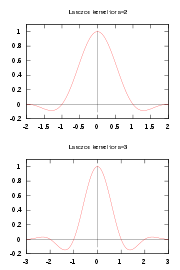
Window function
In signal processing, a window function is a mathematical function that is zero-valued outside of some chosen interval. For instance, a function that is constant inside the interval and zero elsewhere is called a rectangular window, which describes the shape of its graphical representation...
by the Lanczos window. The Lanczos window is the central lobe of a horizontally-stretched sinc, for
. Due to its form, the Lanczos window is also called the sinc window.
Thus the Lanczos filter, on its interval, is a product of two sinc functions. The resulting function is then used as a convolution kernel to resample the input field. In one dimension, its formula is given by:
with a positive integer, typically 2 or 3, controlling the size of the kernel. The parameter corresponds to the number of lobes of sinc, as the normalized sinc has zeros at integers; thus corresponds to just the (positive) central lobe, while has the central lobe and the second lobe on each side, which are negative.
For any positive value of , the Lanczos window and Lanczos filter are continuous and differentiable even at the ends where they to go zero. In the case of positive integer values of , both sinc functions go to zero at the edge, so the edge of the Lanczos filter is zero to second order, which means its derivative is also continuous, and it is differentiable to second order. Thus integer values yield a smoother cutoff, with no corner, which is why integers are generally used.
In the above, we can expand the sinc terms (for nonzero in the specified range):
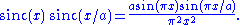
Lanczos filter's kernel in two dimensions is simply the product of two one-dimensional kernels:
Interpolation formulas
Given a one-dimensional function I(x) defined at integer points, an interpolated value at an arbitrary point x0 is given by a convolutionConvolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
with Lanczos kernel:
where a is the size of the filter. The bounds of this sum are such that the kernel is zero outside of them.
Given a two-dimension function I(x, y) defined at integer points (e.g. intensities of pixels in a digital image), the corresponding interpolation formula is:
-
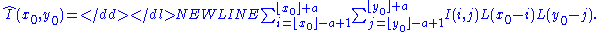
Evaluation
The Lanczos filter has been compared with other filters, particularly other windowing of the sinc filter.png) Sinc filterIn signal processing, a sinc filter is an idealized filter that removes all frequency components above a given bandwidth, leaves the low frequencies alone, and has linear phase...
Sinc filterIn signal processing, a sinc filter is an idealized filter that removes all frequency components above a given bandwidth, leaves the low frequencies alone, and has linear phase...
.
Some have found the Lanczos (with a = 2) the "best compromise in terms of reduction of aliasing, sharpness, and minimal ringing", compared with truncated sinc and the Barlett, cosine, and Hann windowed sinc, for decimation and interpolation of 2-dimensional image data.
It has also been recommended by Jim BlinnJim BlinnJames F. Blinn is a computer scientist who first became widely known for his work as a computer graphics expert at NASA's Jet Propulsion Laboratory , particularly his work on the pre-encounter animations for the Voyager project, his work on the Carl Sagan Cosmos documentary series and the research...
for graphics purposes, with a = 3, saying that it "keeps low frequencies and rejects high frequencies better than any (achievable) filter we've seen so far;" Blinn characterizes himself and others who prefer such filters as "negative lobists" for their preference for such filters more optimized for frequency response than for ringing.
It is used a popular filter for "upscaling" videos in various media utilities, such as AviSynthAviSynthAviSynth is a frameserver program for Microsoft Windows developed by Ben Rudiak-Gould, Edwin van Eggelen, Klaus Post, Richard Berg, Ian Brabham and others. It is free software under GNU GPL license.-Scripting video editor:...
and FFmpegFFmpegFFmpeg is a free software project that produces libraries and programs for handling multimedia data. The most notable parts of FFmpeg are libavcodec, an audio/video codec library used by several other projects, libavformat, an audio/video container mux and demux library, and the ffmpeg command line...
.
Limitations
Because the kernel assumes negative values for a > 1, output values can be negative even with non-negative input. Negative values are out of bounds for image signals and cause clipping artifactsClipping (signal processing)Clipping is a form of distortion that limits a signal once it exceeds a threshold. Clipping may occur when a signal is recorded by a sensor that has constraints on the range of data it can measure, it can occur when a signal is digitized, or it can occur any other time an analog or digital signal...
. Negative lobes also induce ringing artifactsRinging artifactsIn signal processing, particularly digital image processing, ringing artifacts are artifacts that appear as spurious signals near sharp transitions in a signal. Visually, they appear as bands or "ghosts" near edges; audibly, they appear as "echos" near transients, particularly sounds from...
. In some applications, the clipping artifacts can be overcome by transforming the data to a logarithmic domain prior to filtering. In this case the low pass filter will compute a geometric mean, rather than an arithmetic mean.
However, both undershoot and ringing are reduced compared to the (non-windowed) sinc filter, due to the windowing; the ringing is particularly small, as the positive side lobe size demonstrates, especially for a = 2.
In visual processing
A common misconception is that the sinc filter should be the best possible image filter, because of its ideal frequency response. This is only true for bandlimited signals which were sampled after an antialiasing filter, which is not typically the case for images. The human eye does not detect frequency directly (unlike the ear). However, vision utilizes specialized receptor patterns that detect things like localization, edge contrast and contour. The special role of edge contrast in vision is why the negative lobe of the Lanczos filter helps increase perceived sharpnessAcutanceIn photography, acutance is the edge contrast of an image. Acutance is related to the amplitude of the derivative of brightness with respect to space...
even though the halo it creates is an artifact.
As spatial localization and frequency localization are inversely related, visual filters require a trade-off. Good frequency filtering limits aliasing; good localization provides strong edges.
See also
- Bicubic interpolationBicubic interpolationIn mathematics, bicubic interpolation is an extension of cubic interpolation for interpolating data points on a two dimensional regular grid. The interpolated surface is smoother than corresponding surfaces obtained by bilinear interpolation or nearest-neighbor interpolation...
- Bilinear interpolationBilinear interpolationIn mathematics, bilinear interpolation is an extension of linear interpolation for interpolating functions of two variables on a regular grid. The interpolated function should not use the term of x^2 or y^2, but x y, which is the bilinear form of x and y.The key idea is to perform linear...
- Spline interpolationSpline interpolationIn the mathematical field of numerical analysis, spline interpolation is a form of interpolation where the interpolant is a special type of piecewise polynomial called a spline. Spline interpolation is preferred over polynomial interpolation because the interpolation error can be made small even...
- Nearest-neighbor interpolation
- Sinc filterSinc filterIn signal processing, a sinc filter is an idealized filter that removes all frequency components above a given bandwidth, leaves the low frequencies alone, and has linear phase...
External links
- Anti-Grain Geometry examples: image_transforms.cpp shows comparisons of repeatedly resampling an image with various kernels.
- Bicubic interpolation