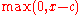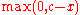
Multivariate adaptive regression splines
Encyclopedia
Multivariate adaptive regression splines (MARS) is a form of regression analysis
introduced by Jerome Friedman in 1991. It is a non-parametric regression technique
and can be seen as an extension of linear model
s that
automatically models non-linearities and interactions.
The term "MARS" is trademarked and licensed to Salford Systems.
Here there is only one independent variable
, so the x matrix is just a single column. Given these measurements, we would like to build a model which predicts the expected y for a given x.
A linear model
for the above data is
Regression analysis
In statistics, regression analysis includes many techniques for modeling and analyzing several variables, when the focus is on the relationship between a dependent variable and one or more independent variables...
introduced by Jerome Friedman in 1991. It is a non-parametric regression technique
and can be seen as an extension of linear model
Linear model
In statistics, the term linear model is used in different ways according to the context. The most common occurrence is in connection with regression models and the term is often taken as synonymous with linear regression model. However the term is also used in time series analysis with a different...
s that
automatically models non-linearities and interactions.
The term "MARS" is trademarked and licensed to Salford Systems.
The basics
This section introduces MARS using a few examples. We start with a set of data: a matrix of input variables x, and a vector of the observed responses y, with a response for each row in x. For example, the data could be:| x | y |
|---|---|
| 10.5 | 16.4 |
| 10.7 | 18.8 |
| 10.8 | 19.7 |
| ... | ... |
| 20.6 | 77.0 |
Here there is only one independent variable
Dependent and independent variables
The terms "dependent variable" and "independent variable" are used in similar but subtly different ways in mathematics and statistics as part of the standard terminology in those subjects...
, so the x matrix is just a single column. Given these measurements, we would like to build a model which predicts the expected y for a given x.
Linear model
In statistics, the term linear model is used in different ways according to the context. The most common occurrence is in connection with regression models and the term is often taken as synonymous with linear regression model. However the term is also used in time series analysis with a different...
for the above data is
-
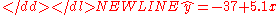
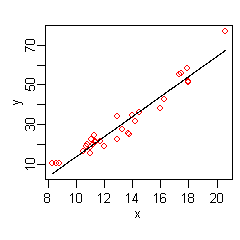
The hat on the
indicates that 
is estimated from the data. The figure on the right shows a plot of this function:
a line giving the predicted
versus x, with the original values of y shown as red dots.
The data at the extremes of x indicates that the relationship between y and x may be non-linear (look at the red dots relative to the regression line at low and high values of x). We thus turn to MARS to automatically build a model taking into account non-linearities. MARS software constructs a model from the given x and y as follows
-
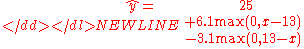
The figure on the right shows a plot of this function: the predicted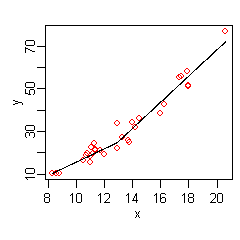
versus x, with the original values of y once again shown as red dots. The predicted response is now a better fit to the original y values.
MARS has automatically produced a kink
in the predicted y to take into account non-linearity.
The kink is produced by hinge functions.
The hinge functions are the expressions starting with
(where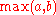
is
if 
, else 
).
Hinge functions are described in more detail below.
In this simple example, we can easily see from the plot that
the y has a non-linear relationship with x
(and might perhaps guess that y varies with the square of x).
However, in general there will be multiple
independent variablesDependent and independent variablesThe terms "dependent variable" and "independent variable" are used in similar but subtly different ways in mathematics and statistics as part of the standard terminology in those subjects...
,
and the relationship between y and these variables will be unclear
and not easily visible by plotting.
We can use MARS to discover that non-linear relationship.
An example MARS expression with multiple variables is
-
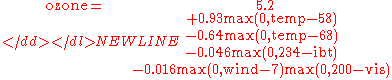
This expression models air pollution (the ozone level)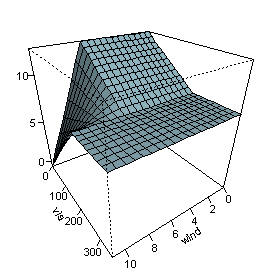
as a function of the temperature and a few other variables.
Note that the last term in the formula (on the last line)
incorporates an interaction between
and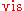
.
The figure on the right plots the predicted
as 
and
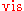vary,
with the other variables fixed at their median values.
The figure shows that wind does not affect the ozone
level unless visibility is low.
We see that MARS can build quite flexible regression surfaces
by combining hinge functions.
The MARS model
MARS builds models of the form
-
.
The model is a weighted sum of basis functions
.
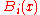Each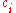
is a constant coefficient.
For example, each line in the formula for ozone above is one basis function
multiplied by its coefficient.
Each basis functionBasis functionIn mathematics, a basis function is an element of a particular basis for a function space. Every continuous function in the function space can be represented as a linear combination of basis functions, just as every vector in a vector space can be represented as a linear combination of basis...
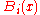
takes one of the following three forms:
1) a constant 1. There is just one such term, the intercept.
In the ozone formula above, the intercept term is 5.2.
2) a hinge function.
A hinge function has the form
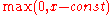
or
.
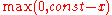MARS automatically selects variables
and values of those variables for knots of the hinge functions.
Examples of such basis functions can be seen
in the middle three lines of the ozone formula.
3) a product of two or more hinge functions.
These basis function can model interaction between two or more variables.
An example is the last line of the ozone formula.
Hinge functions
Hinge functions are a key part of MARS models.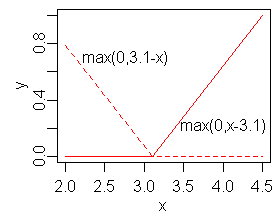
A hinge function takes the form
or
where
is a constant, called the knot.
The figure on the right shows a mirrored pair of hinge functions with a knot at 3.1.
A hinge function is zero for part of its range, so
can be used to partition the data into disjoint regions,
each of which can be treated independently.
Thus for example
a mirrored pair of hinge functions in the expression-
creates the piecewisePiecewiseOn mathematics, a piecewise-defined function is a function whose definition changes depending on the value of the independent variable...
linear graph shown for the
simple MARS model in the previous section.
One might assume that only piecewise
linear functions can be formed from hinge functions, but
hinge functions can be multiplied together to form non-linear functions.
Hinge functions are also called hockey stickIce hockey stickAn ice hockey stick is a piece of equipment used in ice hockey to shoot, pass, and carry the puck. Ice hockey sticks are approximately 150–200 cm long, composed of a long, slender shaft with a flat extension at one end called the blade. The blade is the part of the stick used to contact the...
functions.
Instead of the
notation used in this article,
hinge functions are often represented by
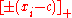
where
means take the positive part.
Alternatively, the hinge function may be defined as
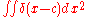
where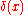
is the dirac delta function defined as an impulse at the origin whose integral is 1.
The model building process
MARS builds a model in two phases:
the forward and the backward pass.
This two stage approach is the same as that used by
recursive partitioningRecursive partitioningRecursive partitioning is a statistical method for multivariable analysis. Recursive partitioning creates a decision tree that strives to correctly classify members of the population based on several dichotomous dependent variables....
trees.
The forward pass
MARS starts with a model which consists of just the intercept term
(which is the mean of the response values).
MARS then repeatedly adds basis function in pairs to the model.
At each step it finds the pair of basis functions that
gives the maximum reduction in sum-of-squares
residualErrors and residuals in statisticsIn statistics and optimization, statistical errors and residuals are two closely related and easily confused measures of the deviation of a sample from its "theoretical value"...
error
(it is a greedy algorithmGreedy algorithmA greedy algorithm is any algorithm that follows the problem solving heuristic of making the locally optimal choice at each stagewith the hope of finding the global optimum....
).
The two basis functions in the pair
are identical except that a different
side of a mirrored hinge function is used for each function.
Each new basis function consists of
a term already in the model
(which could perhaps be the intercept i.e. a constant 1)
multiplied by a new hinge function.
A hinge function is defined by a variable and a knot,
so to add a new basis function, MARS must search over
all combinations of the following:
1) existing terms (called parent terms in this context)
2) all variables (to select one for the new basis function)
3) all values of each variable (for the knot of the new hinge function).
This process of adding terms continues until
the change in residual error is too small to continue
or until the maximum number of terms is reached.
The maximum number of terms
is specified by the user before model building starts.
The search at each step is done in a brute forceBrute-force searchIn computer science, brute-force search or exhaustive search, also known as generate and test, is a trivial but very general problem-solving technique that consists of systematically enumerating all possible candidates for the solution and checking whether each candidate satisfies the problem's...
fashion,
but a key aspect of MARS is that
because of the nature of hinge functions
the search can be done relatively
quickly using a fast least-squares update technique.
Actually, the search is not quite brute force.
The search can be sped up with a heuristic
that reduces the number
of parent terms to consider at each step
("Fast MARS"
).
The backward pass
The forward pass usually builds an overfit model.
(An overfit model has a good fit to the data used to build
the model but will not generalize well to new data.)
To build a model with better generalization ability,
the backward pass prunes the model.
It removes terms one by one,
deleting the least effective term at each step
until it finds the best submodel.
Model subsets are compared using the GCV criterion described below.
The backward pass has an advantage over the forward pass:
at any step it can choose any term to delete,
whereas the forward pass
at each step can only see the next pair of terms.
The forward pass adds terms in pairs,
but the backward pass typically discards one side of the pair
and so terms are often not seen in pairs in the final model.
A paired hinge can be seen in
the equation for
in the
first MARS example above;
there are no complete pairs retained in the ozone example.
Generalized cross validation (GCV)
The backward pass uses GCV to compare the performance of model subsets in order to choose the best subset: lower values of GCV are better.
The GCV is a form of
regularizationRegularization (machine learning)In statistics and machine learning, regularization is any method of preventing overfitting of data by a model. It is used for solving ill-conditioned parameter-estimation problems...
:
it trades off goodness-of-fit against model complexity.
The raw residual sum-of-squaresResidual sum of squaresIn statistics, the residual sum of squares is the sum of squares of residuals. It is also known as the sum of squared residuals or the sum of squared errors of prediction . It is a measure of the discrepancy between the data and an estimation model...
(RSS)
on the training data is inadequate for comparing models, because
the RSS always increases as MARS terms are dropped.
In other words, if the RSS were used to
compare models, the backward pass would always choose the largest model.
The formula for the GCV is
GCV = RSS / (N * (1 -
/ N)^2)
where
is the residual sum-of-squares
measured on the training data and
is the
number of observations (the number of rows in the x matrix).
The
is defined in
the MARS context as
= 
+ 
* (
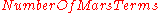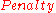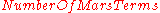- 1 ) / 2
where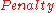
is about 2 or 3 (the
MARS software allows the user to preset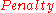
).
Note that
(
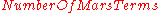- 1 ) / 2
is the number of hinge-function knots,
so the formula penalizes the addition of knots.
Thus the GCV formula adjusts (i.e. increases) the training RSS to take into
account the flexibility of the model.
Generalized Cross Validation is so named because
it uses a formula to approximate the error
that would be determined by leave-one-out validation.
GCVs were introduced by Craven and
WahbaGrace WahbaGrace Wahba is the I. J. Schoenberg Professor of Statistics at the University of Wisconsin–Madison. She is a pioneer in methods for smoothing noisy data...
and extended by Friedman for MARS.
Constraints
One constraint has already been mentioned: the user
can specify the maximum number of terms in the forward pass.
A further constraint can be placed on the forward pass
by specifying a maximum allowable degree of interaction.
Typically only one or two degrees of interaction are allowed,
but higher degrees can be used when the data warrants it.
The maximum degree of interaction in the first MARS example
above is one (i.e. no interactions or an additive model);
in the ozone example it is two.
Other constraints on the forward pass are possible.
For example, the user can specify that interactions are allowed
only for certain input variables.
Such constraints could make sense because of knowledge
of the process that generated the data.
Pros and cons
No regression modeling technique is best for all situations.
The guidelines below are intended to give an idea of the pros and cons of MARS,
but there will be exceptions to the guidelines.
It is useful to compare MARS to recursive partitioningRecursive partitioningRecursive partitioning is a statistical method for multivariable analysis. Recursive partitioning creates a decision tree that strives to correctly classify members of the population based on several dichotomous dependent variables....
and this is done below.
(Recursive partitioning is also commonly called regression trees,
decision trees, or CART;
see the recursive partitioningDecision tree learningDecision tree learning, used in statistics, data mining and machine learning, uses a decision tree as a predictive model which maps observations about an item to conclusions about the item's target value. More descriptive names for such tree models are classification trees or regression trees...
article for details).
- MARS models are more flexible than linear regressionLinear regressionIn statistics, linear regression is an approach to modeling the relationship between a scalar variable y and one or more explanatory variables denoted X. The case of one explanatory variable is called simple regression...
models.
- MARS models are simple to understand and interpret. Compare the equation for ozone concentration above to, say, the innards of a trained neural networkArtificial neural networkAn artificial neural network , usually called neural network , is a mathematical model or computational model that is inspired by the structure and/or functional aspects of biological neural networks. A neural network consists of an interconnected group of artificial neurons, and it processes...
or a random forestRandom forestRandom forest is an ensemble classifier that consists of many decision trees and outputs the class that is the mode of the class's output by individual trees. The algorithm for inducing a random forest was developed by Leo Breiman and Adele Cutler, and "Random Forests" is their trademark...
.
- MARS can handle both numeric and categorical data. MARS tends to be better than recursive partitioning for numeric data because hinges are more appropriate for numeric variables than the piecewise constant segmentation used by recursive partitioning.
- Building MARS models often requires little or no data preparation. The hinge functions automatically partition the input data, so the effect of outliers is contained. In this respect MARS is similar to recursive partitioningRecursive partitioningRecursive partitioning is a statistical method for multivariable analysis. Recursive partitioning creates a decision tree that strives to correctly classify members of the population based on several dichotomous dependent variables....
which also partitions the data into disjoint regions, although using a different method.
- MARS (like recursive partitioning) does automatic variable selection (meaning it includes important variables in the model and excludes unimportant ones). However, bear in mind that variable selection is not a clean problem and there is usually some arbitrariness in the selection, especially in the presence of collinearityMulticollinearityMulticollinearity is a statistical phenomenon in which two or more predictor variables in a multiple regression model are highly correlated. In this situation the coefficient estimates may change erratically in response to small changes in the model or the data...
and 'concurvity'.
- MARS models tend to have a good bias-variance trade-off. The models are flexible enough to model non-linearity and variable interactions (thus MARS models have fairly low bias), yet the constrained form of MARS basis functions prevents too much flexibility (thus MARS models have fairly low variance).
- MARS is suitable for handling fairly large datasets. It is a routine matter to build a MARS model from an x matrix with, say, 100 predictors and 105 observations. Such a model can be built in about a minute on a 1 GHz machine, assuming the maximum degree of interaction of MARS terms is limited to one (i.e. additive terms only). A degree two model with the same data on the same 1 GHz machine takes longer—about 12 minutes. Be aware that these times are highly data dependent. Recursive partitioning is much faster than MARS.
- With MARS models, as with any non-parametric regression, parameter confidence intervals and other checks on the model cannot be calculated directly (unlike linear regressionLinear regressionIn statistics, linear regression is an approach to modeling the relationship between a scalar variable y and one or more explanatory variables denoted X. The case of one explanatory variable is called simple regression...
models). Cross-validation and related techniques must be used for validating the model instead.
- MARS models do not give as good fits as boostedBoostingBoosting is a machine learning meta-algorithm for performing supervised learning. Boosting is based on the question posed by Kearns: can a set of weak learners create a single strong learner? A weak learner is defined to be a classifier which is only slightly correlated with the true classification...
trees, but can be built much more quickly and are more interpretable. (An 'interpretable' model is in a form that makes it clear what the effect of each predictor is.)
- The
earth,mda, andpolsplineimplementations do not allow missing values in predictors, but free implementations of regression trees (such asrpartandparty) do allow missing values using a technique called surrogate splits.
See also
- Linear regressionLinear regressionIn statistics, linear regression is an approach to modeling the relationship between a scalar variable y and one or more explanatory variables denoted X. The case of one explanatory variable is called simple regression...
- Segmented regressionSegmented regressionSegmented regression is a method in regression analysis in which the independent variable is partitioned into intervals and a separate line segment is fit to each interval. Segmented or piecewise regression analysis can also be performed on multivariate data by partitioning the various independent...
- Generalized linear modelGeneralized linear modelIn statistics, the generalized linear model is a flexible generalization of ordinary linear regression. The GLM generalizes linear regression by allowing the linear model to be related to the response variable via a link function and by allowing the magnitude of the variance of each measurement to...
s (GLMs) can be incorporated into MARS models by applying a link function after the MARS model is built. Thus, for example, MARS models can incorporate logistic regressionLogistic regressionIn statistics, logistic regression is used for prediction of the probability of occurrence of an event by fitting data to a logit function logistic curve. It is a generalized linear model used for binomial regression...
to predict probabilities. - Non-linear regressionNonlinear regressionIn statistics, nonlinear regression is a form of regression analysis in which observational data are modeled by a function which is a nonlinear combination of the model parameters and depends on one or more independent variables...
is used when the underlying form of the function is known and regression is used only to estimate the parameters of that function. MARS, on the other hand, estimates the functions themselves, albeit with severe constraints on the nature of the functions. (These constraints are necessary because discovering a model from the data is an inverse problemInverse problemAn inverse problem is a general framework that is used to convert observed measurements into information about a physical object or system that we are interested in...
and is not well-posedWell-posed problemThe mathematical term well-posed problem stems from a definition given by Jacques Hadamard. He believed that mathematical models of physical phenomena should have the properties that# A solution exists# The solution is unique...
without constraints on the model.) - Recursive partitioningRecursive partitioningRecursive partitioning is a statistical method for multivariable analysis. Recursive partitioning creates a decision tree that strives to correctly classify members of the population based on several dichotomous dependent variables....
(commonly called CART). MARS can be seen as a generalization of recursive partioning that allows the model to better handle numerical (i.e. non-categorical) data. - Generalized additive modelGeneralized additive modelIn statistics, the generalized additive model is a statistical model developed by Trevor Hastie and Rob Tibshirani for blending properties of generalized linear models with additive models....
s. From the user's perspective GAMs are similar to MARS but (a) fit smooth loessLocal regressionLOESS, or LOWESS , is one of many "modern" modeling methods that build on "classical" methods, such as linear and nonlinear least squares regression. Modern regression methods are designed to address situations in which the classical procedures do not perform well or cannot be effectively applied...
or polynomial splinesSpline (mathematics)In mathematics, a spline is a sufficiently smooth piecewise-polynomial function. In interpolating problems, spline interpolation is often preferred to polynomial interpolation because it yields similar results, even when using low-degree polynomials, while avoiding Runge's phenomenon for higher...
instead of MARS basis functions, and (b) do not automatically model variable interactions. The fitting method used internally by GAMs is very different from that of MARS. - Rational function modeling
- Spline interpolationSpline interpolationIn the mathematical field of numerical analysis, spline interpolation is a form of interpolation where the interpolant is a special type of piecewise polynomial called a spline. Spline interpolation is preferred over polynomial interpolation because the interpolation error can be made small even...
Free
- Several RR (programming language)R is a programming language and software environment for statistical computing and graphics. The R language is widely used among statisticians for developing statistical software, and R is widely used for statistical software development and data analysis....
packages fit MARS-type models: - Matlab code:
Commercial
- MARS from Salford Systems
- STATISTICA Data Miner from StatSoft
Further reading
- Hastie T., Tibshirani R., and Friedman J.H. (2009) The Elements of Statistical Learning, 2nd edition. Springer, ISBN 978-0-387-84857-0 (has a section on MARS)
- Faraway J. (2005) Extending the Linear Model with R, CRC, ISBN 978-1-58488-424-8 (has an example using MARS with R)
- Heping Zhang and Burton H. Singer (2010) Recursive Partitioning and Applications, 2nd edition. Springer, ISBN 978-1441968234 (has a chapter on MARS and discusses some tweaks to the algorithm)
- Denison D.G.T., Holmes C.C., Mallick B.K., and Smith A.F.M. (2004) Bayesian Methods for Nonlinear Classification and Regression, Wiley, ISBN 978-0-471-49036-4
- Berk R.A. (2008) Statistical learning from a regression persepective, Springer, ISBN 978-0-387-77500-5
- MARS models are more flexible than linear regression
-
-
-
