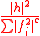Multiplier ideal
Encyclopedia
In commutative algebra
, the multiplier ideal associated to a sheaf
of ideals
over a complex
variety
and a real number c consists (locally) of the functions h such that
is locally integrable
, where the fi are a finite set of local generators of the ideal. Multiplier ideals were independently introduced by (who worked with sheaves over complex manifolds rather than ideals) and , who called them adjoint ideals.
Multiplier ideals are discussed in the survey articles , , and .
Commutative algebra
Commutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
, the multiplier ideal associated to a sheaf
Sheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
of ideals
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
over a complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
variety
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
and a real number c consists (locally) of the functions h such that
is locally integrable
Locally integrable function
In mathematics, a locally integrable function is a function which is integrable on any compact set of its domain of definition. Their importance lies on the fact that we do not care about their behavior at infinity.- Formal definition :...
, where the fi are a finite set of local generators of the ideal. Multiplier ideals were independently introduced by (who worked with sheaves over complex manifolds rather than ideals) and , who called them adjoint ideals.
Multiplier ideals are discussed in the survey articles , , and .