
MinHash
Encyclopedia
In computer science
, MinHash (or the min-wise independent permutations locality sensitive hashing
scheme) is a technique for quickly estimating how similar two sets are. The scheme was invented by , and initially used in the AltaVista
search engine to detect duplicate web pages and eliminate them from search results.
It has also been applied in large-scale clustering
problems, such as clustering documents by the similarity of their sets of words.
of two sets and is defined to be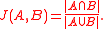
It is a number between 0 and 1; it is 0 when the two sets are disjoint, 1 when they are equal, and strictly between 0 and 1 otherwise. It is a commonly used indicator of the similarity between two sets: two sets are more similar when their Jaccard index is closer to 1, and more dissimilar when their Jaccard index is closer to 0.
Let h be a hash function
that maps the members of and to distinct integers, and for any set S define to be the member of with the minimum value of . Then exactly when the minimum hash value of the union lies in the intersection .
Therefore,
In other words, if is a random variable that is one when and zero otherwise, then is an unbiased estimator
of , although it has too high a variance
to be useful on its own. The idea of the MinHash scheme is to reduce the variance by averaging together several variables constructed in the same way.
To estimate using this version of the scheme, let y be the number of hash functions for which , and use as the estimate. This estimate is the average of different 0-1 random variables, each of which is one when and zero otherwise, and each of which is an unbiased estimator of . Therefore, their average is also an unbiased estimator, and by standard Chernoff bound
s for sums of 0-1 random variables, its expected error is . Therefore, for any constant there is a constant such that the expected error of the estimate is at most . For example, 400 hashes would be required to estimate with an expected error less than or equal to .05.
define to be the subset of the members of that have the smallest values of . This subset is used as a signature for the set , and the similarity of any two sets is estimated by comparing their signatures.
Specifically, let A and B be any two sets.
Then is a set of k elements of , and if h is a random function then any subset of k elements is equally likely to be chosen; that is, is a simple random sample
of . The subset is the set of members of that belong to the intersection . Therefore, ||/ is an unbiased estimator of . The difference between this estimator and the estimator produced by multiple hash functions is that always has exactly members, whereas the multiple hash functions may lead to a smaller number of sampled elements due to the possibility that two different hash functions may have the same minima. However, when is small relative to the sizes of the sets, this difference is negligible.
By standard Chernoff bound
s for sampling without replacement, this estimator has expected error , matching the performance of the multiple-hash-function scheme.
on elements, where is the total number of distinct elements in the union of all of the sets to be compared.
But because there are different permutations, it would require bits just to specify a truly random permutation, an infeasibly large number for even moderate values of . Because of this fact, by analogy to the theory of universal hashing
, there has been significant work on finding a family of permutations that is "min-wise independent", meaning that for any subset of the domain, any element is equally likely to be the minimum. It has been established that a min-wise independent family of permutations must include at least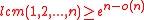
different permutations, and therefore that it needs bits to specify a single permutation, still infeasibly large.
Because of this impracticality, two variant notions of min-wise independence have been introduced: restricted min-wise independent permutations families, and approximate min-wise independent families.
Restricted min-wise independence is the min-wise independence property restricted to certain sets of cardinality at most .
Approximate min-wise independence has at most a fixed probability of varying from full independence.
used MinHash as part of a scheme for the detection of plagiarism
in digital documents, by finding pieces of text that were copied from some large database of documents. Their scheme involves representing a document as the set of its substrings of a given length, partitioning the document into larger fixed-length windows, and using the substring with the minimum hash value as a representative value for each window. If a copied portion of text is longer than twice the window length, then its representative value will be sure to match one of the representatives stored in the database, and that window can be examined to determine how much of it was copied.
In data mining
, use MinHash as a tool for association rule learning
. Given a database in which each entry has multiple attributes (viewed as a 0-1 matrix with a row per database entry and a column per attribute) they use MinHash-based approximations to the Jaccard index to identify candidate pairs of attributes that frequently co-occur, and then compute the exact value of the index for only those pairs to determine the ones whose frequencies of co-occurrence are below a given strict threshold.
, a collection of techniques for using hash functions to map large sets of objects down to smaller hash values in such a way that, when two objects have a small distance to each other, their hash values are likely to be the same. In this instance, the signature of a set may be seen as its hash value. Other locality sensitive hashing techniques exist for Hamming distance
between sets and cosine distance between vectors; locality sensitive hashing has important applications in nearest neighbor search
algorithms.
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, MinHash (or the min-wise independent permutations locality sensitive hashing
Locality sensitive hashing
Locality-sensitive hashing is a method of performing probabilistic dimension reduction of high-dimensional data. The basic idea is to hash the input items so that similar items are mapped to the same buckets with high probability .-Definition:An LSH family \mathcal F is defined fora...
scheme) is a technique for quickly estimating how similar two sets are. The scheme was invented by , and initially used in the AltaVista
AltaVista
AltaVista is a web search engine owned by Yahoo!. AltaVista was once one of the most popular search engines but its popularity declined with the rise of Google...
search engine to detect duplicate web pages and eliminate them from search results.
It has also been applied in large-scale clustering
Clustering
Clustering can refer to the following:In demographics:* Clustering , the gathering of various populations based on factors such as ethnicity, economics or religion.In graph theory:...
problems, such as clustering documents by the similarity of their sets of words.
Jaccard similarity and minimum hash values
The Jaccard similarity coefficientJaccard index
The Jaccard index, also known as the Jaccard similarity coefficient , is a statistic used for comparing the similarity and diversity of sample sets....
of two sets and is defined to be
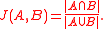
It is a number between 0 and 1; it is 0 when the two sets are disjoint, 1 when they are equal, and strictly between 0 and 1 otherwise. It is a commonly used indicator of the similarity between two sets: two sets are more similar when their Jaccard index is closer to 1, and more dissimilar when their Jaccard index is closer to 0.
Let h be a hash function
Hash function
A hash function is any algorithm or subroutine that maps large data sets to smaller data sets, called keys. For example, a single integer can serve as an index to an array...
that maps the members of and to distinct integers, and for any set S define to be the member of with the minimum value of . Then exactly when the minimum hash value of the union lies in the intersection .
Therefore,
In other words, if is a random variable that is one when and zero otherwise, then is an unbiased estimator
Bias of an estimator
In statistics, bias of an estimator is the difference between this estimator's expected value and the true value of the parameter being estimated. An estimator or decision rule with zero bias is called unbiased. Otherwise the estimator is said to be biased.In ordinary English, the term bias is...
of , although it has too high a variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
to be useful on its own. The idea of the MinHash scheme is to reduce the variance by averaging together several variables constructed in the same way.
Variant with many hash functions
The simplest version of the minhash scheme uses different hash functions, where is a fixed integer parameter, and represents each set by the values of for these functions.To estimate using this version of the scheme, let y be the number of hash functions for which , and use as the estimate. This estimate is the average of different 0-1 random variables, each of which is one when and zero otherwise, and each of which is an unbiased estimator of . Therefore, their average is also an unbiased estimator, and by standard Chernoff bound
Chernoff bound
In probability theory, the Chernoff bound, named after Herman Chernoff, gives exponentially decreasing bounds on tail distributions of sums of independent random variables...
s for sums of 0-1 random variables, its expected error is . Therefore, for any constant there is a constant such that the expected error of the estimate is at most . For example, 400 hashes would be required to estimate with an expected error less than or equal to .05.
Variant with a single hash function
It may be computationally expensive to compute multiple hash functions, but a related version of MinHash scheme avoids this penalty by using only a single hash function and uses it to select multiple values from each set rather than selecting only a single minimum value per hash function. Let be a hash function, and let be a fixed integer. If is any set of or more values in the domain of ,define to be the subset of the members of that have the smallest values of . This subset is used as a signature for the set , and the similarity of any two sets is estimated by comparing their signatures.
Specifically, let A and B be any two sets.
Then is a set of k elements of , and if h is a random function then any subset of k elements is equally likely to be chosen; that is, is a simple random sample
Simple random sample
In statistics, a simple random sample is a subset of individuals chosen from a larger set . Each individual is chosen randomly and entirely by chance, such that each individual has the same probability of being chosen at any stage during the sampling process, and each subset of k individuals has...
of . The subset is the set of members of that belong to the intersection . Therefore, ||/ is an unbiased estimator of . The difference between this estimator and the estimator produced by multiple hash functions is that always has exactly members, whereas the multiple hash functions may lead to a smaller number of sampled elements due to the possibility that two different hash functions may have the same minima. However, when is small relative to the sizes of the sets, this difference is negligible.
By standard Chernoff bound
Chernoff bound
In probability theory, the Chernoff bound, named after Herman Chernoff, gives exponentially decreasing bounds on tail distributions of sums of independent random variables...
s for sampling without replacement, this estimator has expected error , matching the performance of the multiple-hash-function scheme.
Time analysis
The estimator ||/ can be computed in time from the two signatures of the given sets, in either variant of the scheme. Therefore, when and are constants, the time to compute the estimated similarity from the signatures is also constant. The signature of each set can be computed in linear time, so when many pairwise similarities need to be estimated this method can lead to a substantial savings in running time compared to doing a full comparison of the members of each set.Min-wise independent permutations
In order to implement the MinHash scheme as described above, one needs the hash function to define a random permutationPermutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
on elements, where is the total number of distinct elements in the union of all of the sets to be compared.
But because there are different permutations, it would require bits just to specify a truly random permutation, an infeasibly large number for even moderate values of . Because of this fact, by analogy to the theory of universal hashing
Universal hashing
Using universal hashing refers to selecting a hash function at random from a family of hash functions with a certain mathematical property . This guarantees a low number of collisions in expectation, even if the data is chosen by an adversary...
, there has been significant work on finding a family of permutations that is "min-wise independent", meaning that for any subset of the domain, any element is equally likely to be the minimum. It has been established that a min-wise independent family of permutations must include at least
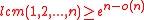
different permutations, and therefore that it needs bits to specify a single permutation, still infeasibly large.
Because of this impracticality, two variant notions of min-wise independence have been introduced: restricted min-wise independent permutations families, and approximate min-wise independent families.
Restricted min-wise independence is the min-wise independence property restricted to certain sets of cardinality at most .
Approximate min-wise independence has at most a fixed probability of varying from full independence.
Applications
The original applications for MinHash involved clustering and eliminating near-duplicates among web documents, represented as sets of the words occurring in those documents. Similar techniques have also been used for clustering and near-duplicate elimination for other types of data, such as images: in the case of image data, an image can be represented as a set of smaller subimages cropped from it, or as sets of more complex image feature descriptions.used MinHash as part of a scheme for the detection of plagiarism
Plagiarism
Plagiarism is defined in dictionaries as the "wrongful appropriation," "close imitation," or "purloining and publication" of another author's "language, thoughts, ideas, or expressions," and the representation of them as one's own original work, but the notion remains problematic with nebulous...
in digital documents, by finding pieces of text that were copied from some large database of documents. Their scheme involves representing a document as the set of its substrings of a given length, partitioning the document into larger fixed-length windows, and using the substring with the minimum hash value as a representative value for each window. If a copied portion of text is longer than twice the window length, then its representative value will be sure to match one of the representatives stored in the database, and that window can be examined to determine how much of it was copied.
In data mining
Data mining
Data mining , a relatively young and interdisciplinary field of computer science is the process of discovering new patterns from large data sets involving methods at the intersection of artificial intelligence, machine learning, statistics and database systems...
, use MinHash as a tool for association rule learning
Association rule learning
In data mining, association rule learning is a popular andwell researched method for discovering interesting relations between variablesin large databases. Piatetsky-Shapirodescribes analyzing and presenting...
. Given a database in which each entry has multiple attributes (viewed as a 0-1 matrix with a row per database entry and a column per attribute) they use MinHash-based approximations to the Jaccard index to identify candidate pairs of attributes that frequently co-occur, and then compute the exact value of the index for only those pairs to determine the ones whose frequencies of co-occurrence are below a given strict threshold.
Related topics
The MinHash scheme may be seen as an instance of locality sensitive hashingLocality sensitive hashing
Locality-sensitive hashing is a method of performing probabilistic dimension reduction of high-dimensional data. The basic idea is to hash the input items so that similar items are mapped to the same buckets with high probability .-Definition:An LSH family \mathcal F is defined fora...
, a collection of techniques for using hash functions to map large sets of objects down to smaller hash values in such a way that, when two objects have a small distance to each other, their hash values are likely to be the same. In this instance, the signature of a set may be seen as its hash value. Other locality sensitive hashing techniques exist for Hamming distance
Hamming distance
In information theory, the Hamming distance between two strings of equal length is the number of positions at which the corresponding symbols are different...
between sets and cosine distance between vectors; locality sensitive hashing has important applications in nearest neighbor search
Nearest neighbor search
Nearest neighbor search , also known as proximity search, similarity search or closest point search, is an optimization problem for finding closest points in metric spaces. The problem is: given a set S of points in a metric space M and a query point q ∈ M, find the closest point in S to q...
algorithms.

