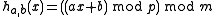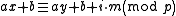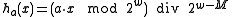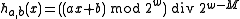Universal hashing
Encyclopedia
Using universal hashing refers to selecting a hash function
at random from a family of hash functions with a certain mathematical property (see definition below). This guarantees a low number of collisions in expectation, even if the data is chosen by an adversary. Many universal families are known (for hashing integers, vectors, strings), and their evaluation is often very efficient. Universal hashing has numerous uses in computer science, for example in implementations of hash table
s, randomized algorithms, and cryptography.
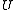into 
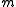bins (labelled 
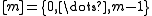). The algorithm will have to handle some data set 
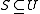of 
keys, which is not known in advance. Usually, the goal of hashing is to obtain a low number of collisions (keys from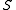 
that land in the same bin). A deterministic hash function cannot offer any guarantee in an adversarial setting if the size of 
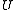is greater than 
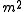, since the adversary may choose 
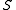to be precisely the preimage
of a bin. This means that all data keys land in the same bin, making hashing useless. Furthermore, a deterministic hash function does not allow for rehashing: sometimes the input data turns out to be bad for the hash function (e.g. there are too many collisions), so one would like to change the hash function.
The solution to these problems is to pick a function randomly from a family of hash functions. A family of functions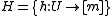
is called a universal family if,
In other words, any two keys of the universe collide with probability at most
when the hash function 
is drawn randomly from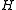 
. This is exactly the probability of collision we would expect if the hash function assigned truly random hash codes to every key. Sometimes, the definition is relaxed to allow collision probability 
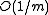. This concept was introduced by Carter and Wegman in 1977, and has found numerous applications in computer science (see, for example ).
Many, but not all, universal families have the following stronger uniform difference property:
Note that the definition of universality is only concerned with whether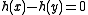
, which counts collisions. The uniform difference property is stronger. Indeed, given a universal family, one can produce a 2-independent hash function
by adding a uniformly distributed random constant with values in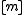
to the hash functions. Since a shift by a constant is typically irrelevant in applications (e.g. hash tables), a careful distinction between universal and 2-independent hash families is often not made.
of 
keys, using a universal family guarantees the following properties.
As the above guarantees hold for any fixed set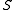
, they hold if the data set is chosen by an adversary. However, the adversary has to make this choice before (or independent of) the algorithm's random choice of a hash function. If the adversary can observe the random choice of the algorithm, randomness serves no purpose, and the situation is the same as deterministic hashing.
The second and third guarantee are typically used in conjunction with rehashing
. For instance, a randomized algorithm may be prepared to handle some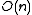
number of collisions. If it observes too many collisions, it chooses another random 
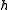from the family and repeats. Universality guarantees that the number of repetitions is a geometric random variable.
.
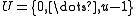The original proposal of Carter and Wegman was to pick a prime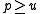
and define
where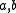
are randomly chosen integers modulo 
with 
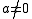. Technically, adding 
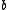is not needed for universality (but it does make the hash function 2-independent).
To see that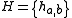
is a universal family, note that 
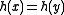only holds when
for some integer
between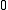 
and 
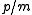. If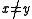 
, their difference, 
is nonzero and has an inverse modulo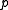 
. Solving for 
,
There are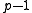
possible choices for 
(since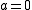 
is excluded) and, varying 
in the allowed range, 
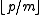possible values for the right hand side. Thus the collision probability is
which tends to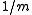
for large 
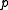as required. This analysis also shows that 
does not have to be randomised in order to have universality.
Another way to see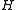
is a universal family is via the notion of statistical distance
. Write the difference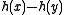
as
Since
is nonzero and 
is uniformly distributed in 
, it follows that 
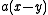modulo 
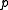is also uniformly distributed in 
. The distribution of 
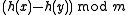is thus almost uniform, up to a difference in probability of 
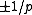between the samples. As a result, the statistical distance to a uniform family is 
, which becomes negligible when 
.
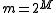. Let 
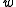be the number of bits in a machine word. Then the hash functions are parametrised over odd positive integers 
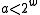(that fit in a word of 
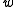bits). To evaluate 
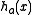, multiply 
by 
modulo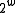 
and then keep the high order 
bits as the hash code. In mathematical notation, this is
and it can be implemented in C
-like programming languages by
This scheme does not satisfy the uniform difference property and is only
-almost-universal; for any 
, 
.
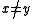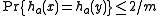To understand the behavior of the hash function,
notice that, if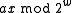
and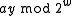 
have the same highest-order 'M' bits, then 
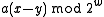has either all 1's or all 0's as its highest order M bits (depending on whether 
or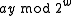 
is larger.
Assume that the least significant set bit of
appears on position 
. Since 
is a random odd integer and odd integers have inverses in the ring
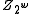, it follows that 
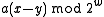will be uniformly distributed among 
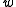-bit integers with the least significant set bit on position 
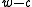. The probability that these bits are all 0's or all 1's is therefore at most 
.
On the other hand, if
, then higher-order M bits of
contain both 0's and 1's, so
it is certain that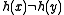
. Finally, if 
then bit 
of
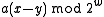is 1 and 
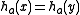if and only if bits 
are also 1, which happens with probability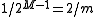 
.
This analysis is tight, as can be shown with the example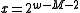
and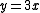 
. To obtain a truly 'universal' hash function, one can use the multiply-add-shift scheme
where
is a random odd positive integer with 
and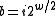 
where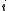 
is chosen at random from 
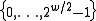. With these choices of 
and 
, 
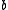for all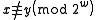 
.
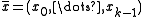of 
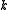machine words (integers of 
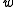bits each). If 
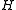is a universal family with the uniform difference property, the following family dating back to Carter and Wegman also has the uniform difference property (and hence is universal):
If
is a power of two, one may replace summation by exclusive or.
In practice, if double-precision arithmetic is available, this is instantiated with the multiply-shift hash family of. Initialize the hash function with a vector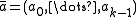
of random odd integers on 
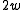bits each. Then if the number of bins is 
for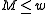 
:
It is possible to halve the number of multiplications, which roughly translates to a two-fold speed-up in practice. Initialize the hash function with a vector
of random odd integers on 
bits each. The following hash family is universal:
If double-precision operations are not available, one can interpret the input as a vector of half-words (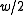
-bit integers). The algorithm will then use 
multiplications, where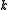 
was the number of half-words in the vector. Thus, the algorithm runs at a "rate" of one multiplication per word of input.
The same scheme can also be used for hashing integers, by interpreting their bits as vectors of bytes. In this variant, the vector technique is known as tabulation hashing
and it provides a practical alternative to multiplication-based universal hashing schemes.
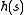is just the length of 
(the zero-padding can be ignored when evaluating the hash function without affecting universality).
Now assume we want to hash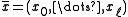
, where a good bound on 
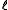is not known a priori. A universal family proposed by.
treats the string
as the coefficients of a polynomial modulo a large prime. If 
, let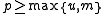 
be a prime and define:
, where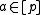 
is uniformly random and 
is chosen randomly from a universal family mapping integer domain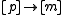 
.
Consider two strings
and let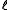 
be length of the longer one; for the analysis, the shorter string is conceptually padded with zeros up to length 
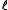. A collision before applying 
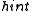implies that 
is a root of the polynomial with coefficients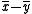 
. This polynomial has at most 
roots modulo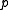 
, so the collision probability is at most 
. The probability of collision through the random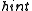 
brings the total collision probability to 
. Thus, if the prime 
is sufficiently large compared to the length of strings hashed, the family is very close to universal (in statistical distance
).
To mitigate the computational penalty of modular arithmetic, two tricks are used in practice :
Hash function
A hash function is any algorithm or subroutine that maps large data sets to smaller data sets, called keys. For example, a single integer can serve as an index to an array...
at random from a family of hash functions with a certain mathematical property (see definition below). This guarantees a low number of collisions in expectation, even if the data is chosen by an adversary. Many universal families are known (for hashing integers, vectors, strings), and their evaluation is often very efficient. Universal hashing has numerous uses in computer science, for example in implementations of hash table
Hash table
In computer science, a hash table or hash map is a data structure that uses a hash function to map identifying values, known as keys , to their associated values . Thus, a hash table implements an associative array...
s, randomized algorithms, and cryptography.
Introduction
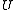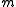Assume we want to map keys from some universe into bins (labelled 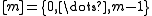). The algorithm will have to handle some data set 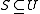of keys, which is not known in advance. Usually, the goal of hashing is to obtain a low number of collisions (keys from 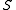that land in the same bin). A deterministic hash function cannot offer any guarantee in an adversarial setting if the size of 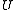is greater than 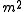, since the adversary may choose 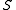to be precisely the preimageImage (mathematics)
In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
of a bin. This means that all data keys land in the same bin, making hashing useless. Furthermore, a deterministic hash function does not allow for rehashing: sometimes the input data turns out to be bad for the hash function (e.g. there are too many collisions), so one would like to change the hash function.
The solution to these problems is to pick a function randomly from a family of hash functions. A family of functions
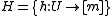is called a universal family if,-
.
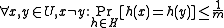In other words, any two keys of the universe collide with probability at most
when the hash function is drawn randomly from 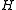. This is exactly the probability of collision we would expect if the hash function assigned truly random hash codes to every key. Sometimes, the definition is relaxed to allow collision probability 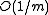. This concept was introduced by Carter and Wegman in 1977, and has found numerous applications in computer science (see, for example ).Many, but not all, universal families have the following stronger uniform difference property:
-
, when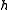 
is drawn randomly from the family 
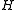, the difference 
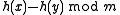is uniformly distributed in 
.
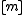Note that the definition of universality is only concerned with whether
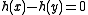, which counts collisions. The uniform difference property is stronger. Indeed, given a universal family, one can produce a 2-independent hash functionK-independent hashing
A family of hash functions is said to be k-independent or k-universal if selecting a hash function at random from the family guarantees that the hash codes of any designated k keys are independent random variables...
by adding a uniformly distributed random constant with values in
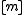to the hash functions. Since a shift by a constant is typically irrelevant in applications (e.g. hash tables), a careful distinction between universal and 2-independent hash families is often not made.Mathematical guarantees
For any fixed set of keys, using a universal family guarantees the following properties.
- For any fixed
in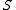 
, the expected number of keys in the bin 
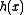is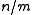 
. When implementing hash tables by chaining, this number is proportional to the expected running time of an operation involving the key 
(for example a query, insertion or deletion). - The expected number of pairs of keys
in 
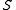with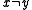 
that collide (
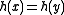) is bounded above by 
, which is of order 
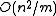. When the number of bins, 
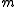, is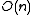 
, the expected number of collisions is 
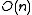. When hashing into 
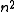bins, there are no collisions at all with probability at least a half. - The expected number of keys in bins with at least
keys in them is bounded above by 
. Thus, if the capacity of each bin is capped to three times the average size (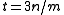
), the total number of keys in overflowing bins is at most 
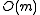. This only holds with a hash family whose collision probability is bounded above by 
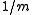. If a weaker definition is used, bounding it by 
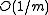, this result is no longer true.
As the above guarantees hold for any fixed set
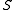, they hold if the data set is chosen by an adversary. However, the adversary has to make this choice before (or independent of) the algorithm's random choice of a hash function. If the adversary can observe the random choice of the algorithm, randomness serves no purpose, and the situation is the same as deterministic hashing.The second and third guarantee are typically used in conjunction with rehashing
Double hashing
Double hashing is a computer programming technique used in hash tables to resolve hash collisions, cases when two different values to be searched for produce the same hash key...
. For instance, a randomized algorithm may be prepared to handle some
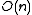number of collisions. If it observes too many collisions, it chooses another random 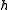from the family and repeats. Universality guarantees that the number of repetitions is a geometric random variable.Constructions
Since any computer data can be represented as one or more machine words, one generally needs hash functions for three types of domains: machine words ("integers"); fixed-length vectors of machine words; and variable-length vectors ("strings").Hashing integers
This section refers to the case of hashing integers that fit in machines words; thus, operations like multiplication, addition, division, etc. are cheap machine-level instructions. Let the universe to be hashed be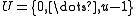.The original proposal of Carter and Wegman was to pick a prime
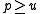and define
where
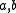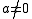are randomly chosen integers modulo with . Technically, adding 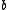is not needed for universality (but it does make the hash function 2-independent).To see that
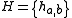is a universal family, note that 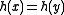only holds when
for some integer
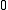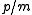between and . If 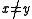, their difference, is nonzero and has an inverse modulo 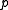. Solving for ,-
.
There are
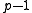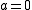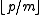possible choices for (since is excluded) and, varying in the allowed range, possible values for the right hand side. Thus the collision probability is
which tends to
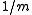for large 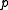as required. This analysis also shows that does not have to be randomised in order to have universality.Another way to see
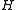is a universal family is via the notion of statistical distanceStatistical distance
In statistics, probability theory, and information theory, a statistical distance quantifies the distance between two statistical objects, which can be two samples, two random variables, or two probability distributions, for example.-Metrics:...
. Write the difference
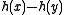as-
.
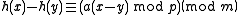Since
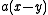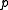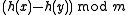is nonzero and is uniformly distributed in , it follows that modulo is also uniformly distributed in . The distribution of is thus almost uniform, up to a difference in probability of 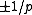between the samples. As a result, the statistical distance to a uniform family is , which becomes negligible when .Avoiding modular arithmetic
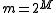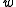The state of the art for hashing integers is the multiply-shift scheme described by Dietzfelbinger et al. in 1997. By avoiding modular arithmetic, this method is much easier to implement and also runs significantly faster in practice (usually by at least a factor of four). The scheme assumes the number of bins is a power of two,. Let be the number of bits in a machine word. Then the hash functions are parametrised over odd positive integers 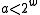(that fit in a word of 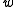bits). To evaluate 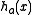, multiply by modulo 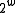and then keep the high order bits as the hash code. In mathematical notation, this is
and it can be implemented in C
C (programming language)
C is a general-purpose computer programming language developed between 1969 and 1973 by Dennis Ritchie at the Bell Telephone Laboratories for use with the Unix operating system....
-like programming languages by
-
(unsigned) (a*x) >> (w-M)
This scheme does not satisfy the uniform difference property and is only
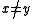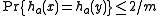-almost-universal; for any , .To understand the behavior of the hash function,
notice that, if
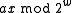and 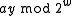have the same highest-order 'M' bits, then 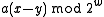has either all 1's or all 0's as its highest order M bits (depending on whether or 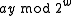is larger.Assume that the least significant set bit of
appears on position . Since is a random odd integer and odd integers have inverses in the ringRing (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
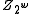, it follows that 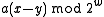will be uniformly distributed among 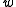-bit integers with the least significant set bit on position 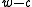. The probability that these bits are all 0's or all 1's is therefore at most .On the other hand, if
, then higher-order M bits of contain both 0's and 1's, soit is certain that
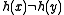. Finally, if then bit of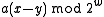 is 1 and 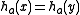if and only if bits are also 1, which happens with probability 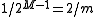.This analysis is tight, as can be shown with the example
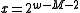and 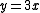. To obtain a truly 'universal' hash function, one can use the multiply-add-shift scheme
where
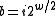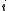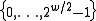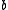is a random odd positive integer with and where is chosen at random from . With these choices of and , for all 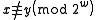.Hashing vectors
This section is concerned with hashing a fixed-length vector of machine words. Interpret the input as a vector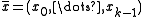 of 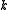machine words (integers of 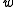bits each). If 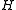is a universal family with the uniform difference property, the following family dating back to Carter and Wegman also has the uniform difference property (and hence is universal):-
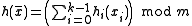, where each 
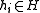is chosen independently at random.
If
is a power of two, one may replace summation by exclusive or.In practice, if double-precision arithmetic is available, this is instantiated with the multiply-shift hash family of. Initialize the hash function with a vector
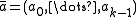of random odd integers on 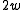bits each. Then if the number of bins is for :-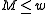
.
It is possible to halve the number of multiplications, which roughly translates to a two-fold speed-up in practice. Initialize the hash function with a vector
of random odd integers on bits each. The following hash family is universal:
-
.
If double-precision operations are not available, one can interpret the input as a vector of half-words (
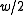-bit integers). The algorithm will then use multiplications, where 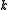was the number of half-words in the vector. Thus, the algorithm runs at a "rate" of one multiplication per word of input.The same scheme can also be used for hashing integers, by interpreting their bits as vectors of bytes. In this variant, the vector technique is known as tabulation hashing
Tabulation hashing
In computer science, tabulation hashing is a method for constructing universal families of hash functions by combining table lookup with exclusive or operations...
and it provides a practical alternative to multiplication-based universal hashing schemes.
Hashing strings
This refers to hashing a variable-sized vector of machine words. If the length of the string can be bounded by a small number, it is best to use the vector solution from above (conceptually padding the vector with zeros up to the upper bound). The space required is the maximal length of the string, but the time to evaluate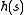 is just the length of (the zero-padding can be ignored when evaluating the hash function without affecting universality).Now assume we want to hash
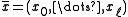, where a good bound on 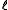is not known a priori. A universal family proposed by.treats the string
as the coefficients of a polynomial modulo a large prime. If , let 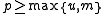be a prime and define:, where 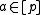is uniformly random and is chosen randomly from a universal family mapping integer domain 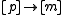.Consider two strings
and let 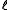be length of the longer one; for the analysis, the shorter string is conceptually padded with zeros up to length 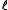. A collision before applying 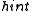implies that is a root of the polynomial with coefficients 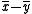. This polynomial has at most roots modulo 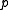, so the collision probability is at most . The probability of collision through the random 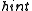brings the total collision probability to . Thus, if the prime is sufficiently large compared to the length of strings hashed, the family is very close to universal (in statistical distanceStatistical distance
In statistics, probability theory, and information theory, a statistical distance quantifies the distance between two statistical objects, which can be two samples, two random variables, or two probability distributions, for example.-Metrics:...
).
To mitigate the computational penalty of modular arithmetic, two tricks are used in practice :
- One chooses the prime
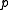to be close to a power of two, such as a Mersenne primeMersenne primeIn mathematics, a Mersenne number, named after Marin Mersenne , is a positive integer that is one less than a power of two: M_p=2^p-1.\,...
. This allows arithmetic modulo
to be implemented without division (using faster operations like addition and shifts). For instance, on modern architectures one can work with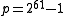 
, while 
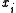's are 32-bit values. - One can apply vector hashing to blocks. For instance, one applies vector hashing to each 16-word block of the string, and applies string hashing to the
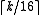results. Since the slower string hashing is applied on a substantially smaller vector, this will essentially be as fast as vector hashing.