Milnor number
Encyclopedia
In mathematics, and particularly singularity theory
, the Milnor number, named after John Milnor
, is an invariant of a function germ.
If f is a complex-valued holomorphic function germ
then the Milnor number of f, denoted μ(f), is either an integer
greater than or equal to zero, or it is infinite. It can be considered both a geometric invariant
and an algebraic invariant. This is why it plays an important role in algebraic geometry
and singularity theory
.
f: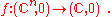
Thus for an n-tuple of complex numbers
we get a complex number
We shall write 
We say that f is singular at a point
if the first order partial derivatives 
are all zero at 
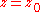. As the name might suggest: we say that a singular point 
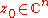is isolated if there exists a sufficiently small neighbourhood
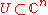of 
such that 
is the only singular point in U. We say that a point is a degenerate singular point, or that f has a degenerate singularity, at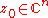 
if 
is a singular point and the Hessian matrix
of all second order partial derivatives has zero determinant
at
:
We assume that f has a degenerate singularity at 0. We can speak about the multiplicity of this degenerate singularity by thinking about how many points are infinitesimally glued. If we now perturb
the image of f in a certain stable way the isolated degenerate singularity at 0 will split up into other isolated singularities which are non-degenerate! The number of such isolated non-degenerate singularities will be the number of points that have been infinitesimally glued.
Precisely, we take another function germ g which is non-singular at the origin and consider the new function germ h := f + εg where ε is very small. When ε = 0 then h = f. The function h is called the morsification of f. It is very difficult to compute the singularities of h, and indeed it may be computationally impossible. This number of points that have been infinitesimally glued, this local multiplicity of f, is exactly the Milnor number of f.
denote the ring
of function germs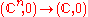
. By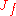 
denote the Jacobian ideal of f: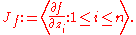
The local algebra of f is then given by the quotient
algebra
Notice that this quotient space will actually be a vector space
, although it may not be finite dimensional. The Milnor number is then equal to the complex dimension of the local algebra:
It follows from Hilbert's Nullstellensatz that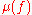
is finite if and only if the origin is an isolated critical point of f; that is, there is a neighbourhood of 0 in 
such that the only critical point of f inside that neighbourhood is at 0.
. The Jacobian ideal is just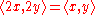 
. We next compute the local algebra: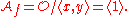
To see why this is true we can use Hadamard's lemma
which says that we can write any function
as
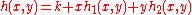
for some constant k and functions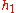
and 
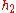in 
(where either 
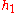or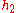 
or both may be exactly zero). So, modulo functional multiples of x and y, we can write h as a constant. The space of constant functions is spanned by 1, hence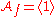 
It follows that μ(f) = 1. It is easy to check that for any function germ g with a non-degenerate singularity at 0 we get μ(g) = 1.
Note that applying this method to a non-singular function germ g we get μ(g) = 0.
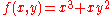, then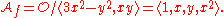
So in this case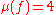
.
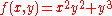then 
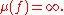
This can be explained by the fact that f is singular at every point of the x-axis.
be a basis
for the local algebra, considered as a vector space. Then a miniversal deformation of f is given by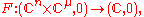
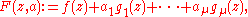
where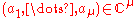
.
These deformations (or unfoldings) are of great interest in much of science.
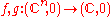are A-equivalent if there exist diffeomorphism
germs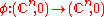
and 
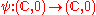such that 
: there exists a diffeomorphic change of variable in both domain and range which takes f to g.
The Milnor number does not offer a complete invariant for function germs. We do have that if f and g are A-equivalent then μ(f) = μ(g).
The converse is false: there exist function germs f and g with μ(f) = μ(g) which are not A-equivalent. To see this consider
and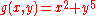 
. We have 
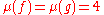but f and g are clearly not A-equivalent since the Hessian matrix
of f is equal to zero while that of g is not (and the rank of the Hessian is an A-invariant, as is easy to see).
Singularity theory
-The notion of singularity:In mathematics, singularity theory is the study of the failure of manifold structure. A loop of string can serve as an example of a one-dimensional manifold, if one neglects its width. What is meant by a singularity can be seen by dropping it on the floor...
, the Milnor number, named after John Milnor
John Milnor
John Willard Milnor is an American mathematician known for his work in differential topology, K-theory and dynamical systems. He won the Fields Medal in 1962, the Wolf Prize in 1989, and the Abel Prize in 2011. Milnor is a distinguished professor at Stony Brook University...
, is an invariant of a function germ.
If f is a complex-valued holomorphic function germ
Germ (mathematics)
In mathematics, the notion of a germ of an object in/on a topological space captures the local properties of the object. In particular, the objects in question are mostly functions and subsets...
then the Milnor number of f, denoted μ(f), is either an integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
greater than or equal to zero, or it is infinite. It can be considered both a geometric invariant
Invariant (mathematics)
In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...
and an algebraic invariant. This is why it plays an important role in algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
and singularity theory
Singularity theory
-The notion of singularity:In mathematics, singularity theory is the study of the failure of manifold structure. A loop of string can serve as an example of a one-dimensional manifold, if one neglects its width. What is meant by a singularity can be seen by dropping it on the floor...
.
Geometric interpretation
Consider a holomorphic complex function germGerm (mathematics)
In mathematics, the notion of a germ of an object in/on a topological space captures the local properties of the object. In particular, the objects in question are mostly functions and subsets...
f:
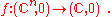
Thus for an n-tuple of complex numbers
we get a complex numberComplex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
We shall write We say that f is singular at a point
if the first order partial derivatives are all zero at 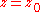. As the name might suggest: we say that a singular point 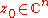is isolated if there exists a sufficiently small neighbourhoodNeighbourhood (mathematics)
In topology and related areas of mathematics, a neighbourhood is one of the basic concepts in a topological space. Intuitively speaking, a neighbourhood of a point is a set containing the point where you can move that point some amount without leaving the set.This concept is closely related to the...
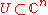of such that is the only singular point in U. We say that a point is a degenerate singular point, or that f has a degenerate singularity, at 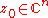if is a singular point and the Hessian matrixHessian matrix
In mathematics, the Hessian matrix is the square matrix of second-order partial derivatives of a function; that is, it describes the local curvature of a function of many variables. The Hessian matrix was developed in the 19th century by the German mathematician Ludwig Otto Hesse and later named...
of all second order partial derivatives has zero determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
at
:We assume that f has a degenerate singularity at 0. We can speak about the multiplicity of this degenerate singularity by thinking about how many points are infinitesimally glued. If we now perturb
Perturbation theory
Perturbation theory comprises mathematical methods that are used to find an approximate solution to a problem which cannot be solved exactly, by starting from the exact solution of a related problem...
the image of f in a certain stable way the isolated degenerate singularity at 0 will split up into other isolated singularities which are non-degenerate! The number of such isolated non-degenerate singularities will be the number of points that have been infinitesimally glued.
Precisely, we take another function germ g which is non-singular at the origin and consider the new function germ h := f + εg where ε is very small. When ε = 0 then h = f. The function h is called the morsification of f. It is very difficult to compute the singularities of h, and indeed it may be computationally impossible. This number of points that have been infinitesimally glued, this local multiplicity of f, is exactly the Milnor number of f.
Algebraic interpretation
Using some algebraic techniques we can calculate the Milnor number of f effortlessly. By denote the ringRing (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
of function germs
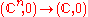. By 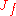denote the Jacobian ideal of f: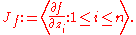The local algebra of f is then given by the quotient
Quotient space (linear algebra)
In linear algebra, the quotient of a vector space V by a subspace N is a vector space obtained by "collapsing" N to zero. The space obtained is called a quotient space and is denoted V/N ....
algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
Notice that this quotient space will actually be a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
, although it may not be finite dimensional. The Milnor number is then equal to the complex dimension of the local algebra:
It follows from Hilbert's Nullstellensatz that
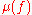is finite if and only if the origin is an isolated critical point of f; that is, there is a neighbourhood of 0 in such that the only critical point of f inside that neighbourhood is at 0.Examples
Here we give some worked examples in two variables. Working with only one is too simple and does not give a feel for the techniques, whereas working with three variables can be quite tricky. Two is a nice number. Also we stick to polynomials. If f is only holomorphic and not a polynomial, then we could have worked with the power series expansion of f.1
Consider a function germ with a non-degenerate singularity at 0, say. The Jacobian ideal is just 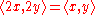. We next compute the local algebra: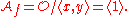To see why this is true we can use Hadamard's lemma
Hadamard's lemma
In mathematics, Hadamard's lemma, named after Jacques Hadamard, is essentially a first-order form of Taylor's theorem, in which we can express a smooth, real-valued function exactly in a convenient manner.-Statement:...
which says that we can write any function
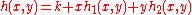
asfor some constant k and functions
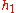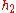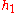and in (where either or 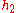or both may be exactly zero). So, modulo functional multiples of x and y, we can write h as a constant. The space of constant functions is spanned by 1, hence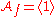 It follows that μ(f) = 1. It is easy to check that for any function germ g with a non-degenerate singularity at 0 we get μ(g) = 1.
Note that applying this method to a non-singular function germ g we get μ(g) = 0.
2
Let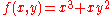, then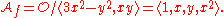So in this case
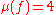.3
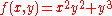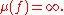
One can show that if then This can be explained by the fact that f is singular at every point of the x-axis.
Versal Deformations
Let f have finite Milnor number μ, and let be a basisBasis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
for the local algebra, considered as a vector space. Then a miniversal deformation of f is given by
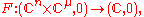
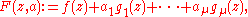
where
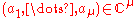.These deformations (or unfoldings) are of great interest in much of science.
Invariance
We can collect function germs together to construct equivalence classes. One standard equivalence is A-equivalence. We say that two function germs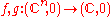 are A-equivalent if there exist diffeomorphismDiffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
germs
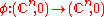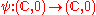and such that : there exists a diffeomorphic change of variable in both domain and range which takes f to g.The Milnor number does not offer a complete invariant for function germs. We do have that if f and g are A-equivalent then μ(f) = μ(g).
The converse is false: there exist function germs f and g with μ(f) = μ(g) which are not A-equivalent. To see this consider
and 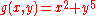. We have 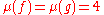but f and g are clearly not A-equivalent since the Hessian matrixHessian matrix
In mathematics, the Hessian matrix is the square matrix of second-order partial derivatives of a function; that is, it describes the local curvature of a function of many variables. The Hessian matrix was developed in the 19th century by the German mathematician Ludwig Otto Hesse and later named...
of f is equal to zero while that of g is not (and the rank of the Hessian is an A-invariant, as is easy to see).