Jacobian ideal
Encyclopedia
In mathematics
the Jacobian ideal or gradient ideal is the ideal
generated by the Jacobian of a function or function germ
.
Let
denote the ring
of smooth functions and f a function in the ring.
The Jacobian ideal of f is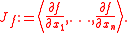
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
the Jacobian ideal or gradient ideal is the ideal
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
generated by the Jacobian of a function or function germ
Germ (mathematics)
In mathematics, the notion of a germ of an object in/on a topological space captures the local properties of the object. In particular, the objects in question are mostly functions and subsets...
.
Let
denote the ringRing (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
of smooth functions and f a function in the ring.
The Jacobian ideal of f is