Mazur manifold
Encyclopedia
In differential topology
, a branch of mathematics, a Mazur manifold is a contractible, compact
, smooth 4-dimensional manifold
which is not diffeomorphic
to the standard 4-ball. The boundary of a Mazur manifold is necessarily a homology 3-sphere
.
Frequently the term Mazur manifold is restricted to a special class of the above definition: 4-manifolds that have a handle decomposition containing exactly three handles: a single 0-handle, a single 1-handle and single 2-handle. This is equivalent to saying the manifold must be of the form
union a 2-handle. An observation of Mazur's shows that the double
of such manifolds is diffeomorphic
to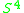
with the standard smooth structure.
of a Mazur manifold is a homotopy 4-sphere
, thus such manifolds are a source of possible counter-examples to the smooth Poincare conjecture in dimension 4
.
gave the first example of such manifolds. He showed that the Brieskorn homology sphere
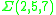is the boundary of a contractible 4-manifold. His results were later generalized by Kirby, Akbulut, Casson, Harer and Stern.
Mazur manifolds have been used by Fintushel and Stern to construct exotic actions of a group of order 2 on the 4-sphere.
Mazur's discovery was something of a surprise for several reasons:
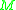be the Mazur manifold, constructed as 
union a 2-handle. Here is a sketch of Mazur's argument that the double
of such a Mazur manifold is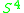
. 
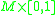is a contractible 5-manifold constructed as 
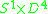union a 2-handle. The 2-handle can be unknotted since the attaching map is a framed knot in the 4-manifold 
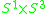. So 
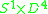union the 2-handle is diffeomorphic to 
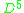. The boundary of 
is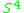 
. But the boundary of 
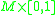is the double
of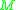
.
Differential topology
In mathematics, differential topology is the field dealing with differentiable functions on differentiable manifolds. It is closely related to differential geometry and together they make up the geometric theory of differentiable manifolds.- Description :...
, a branch of mathematics, a Mazur manifold is a contractible, compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
, smooth 4-dimensional manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
which is not diffeomorphic
Diffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
to the standard 4-ball. The boundary of a Mazur manifold is necessarily a homology 3-sphere
Homology sphere
In algebraic topology, a homology sphere is an n-manifold X having the homology groups of an n-sphere, for some integer n ≥ 1. That is,andTherefore X is a connected space, with one non-zero higher Betti number: bn...
.
Frequently the term Mazur manifold is restricted to a special class of the above definition: 4-manifolds that have a handle decomposition containing exactly three handles: a single 0-handle, a single 1-handle and single 2-handle. This is equivalent to saying the manifold must be of the form
union a 2-handle. An observation of Mazur's shows that the doubleDouble (manifold)
In the subject of manifold theory in mathematics, if M is a manifold with boundary, its double is obtained by gluing two copies of M together along their common boundary...
of such manifolds is diffeomorphic
Diffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
to
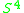with the standard smooth structure.Some properties
In general the doubleDouble (manifold)
In the subject of manifold theory in mathematics, if M is a manifold with boundary, its double is obtained by gluing two copies of M together along their common boundary...
of a Mazur manifold is a homotopy 4-sphere
Homotopy sphere
In algebraic topology, a branch of mathematics, a homotopy sphere is an n-manifold homotopy equivalent to the n-sphere. It thus has the same homotopy groups and the same homology groups, as the n-sphere...
, thus such manifolds are a source of possible counter-examples to the smooth Poincare conjecture in dimension 4
Generalized Poincaré conjecture
In the mathematical area of topology, the term Generalized Poincaré conjecture refers to a statement that a manifold which is a homotopy sphere 'is' a sphere. More precisely, one fixes a...
.
History
Barry MazurBarry Mazur
-Life:Born in New York City, Mazur attended the Bronx High School of Science and MIT, although he did not graduate from the latter on account of failing a then-present ROTC requirement. Regardless, he was accepted for graduate school and received his Ph.D. from Princeton University in 1959,...
gave the first example of such manifolds. He showed that the Brieskorn homology sphere
Homology sphere
In algebraic topology, a homology sphere is an n-manifold X having the homology groups of an n-sphere, for some integer n ≥ 1. That is,andTherefore X is a connected space, with one non-zero higher Betti number: bn...
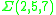is the boundary of a contractible 4-manifold. His results were later generalized by Kirby, Akbulut, Casson, Harer and Stern. Mazur manifolds have been used by Fintushel and Stern to construct exotic actions of a group of order 2 on the 4-sphere.
Mazur's discovery was something of a surprise for several reasons:
- Every homology sphere in dimension
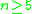bounds a contractible manifold. This follows from the work of Kervaire and the h-cobordismH-cobordismA cobordism W between M and N is an h-cobordism if the inclusion mapsare homotopy equivalences...
theorem. Every homology 4-sphere bounds a contractible 5-manifold (also by Kervaire). Moreover, not every homology 3-sphere bounds a contractible 4-manifold. For example, the Poincare homology sphereHomology sphereIn algebraic topology, a homology sphere is an n-manifold X having the homology groups of an n-sphere, for some integer n ≥ 1. That is,andTherefore X is a connected space, with one non-zero higher Betti number: bn...
does not bound a contractible manifold because the Rochlin invariant provides an obstruction.
- The H-cobordism TheoremH-cobordismA cobordism W between M and N is an h-cobordism if the inclusion mapsare homotopy equivalences...
implies that, at least in dimensions
there is a unique contractible 
-manifold with simply-connected boundary, where uniqueness is up to diffeomorphism. This manifold is the unit ball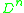 
. It's an open problem as to whether or not 
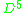admits an exotic smooth structure, but by the h-cobordism theorem, such an exotic smooth structure, if it exists, must restrict to an exotic smooth structure on 
. Whether or not 
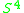admits an exotic smooth structure is equivalent to another open problem, the smooth Poincare conjecture in dimension fourGeneralized Poincaré conjectureIn the mathematical area of topology, the term Generalized Poincaré conjecture refers to a statement that a manifold which is a homotopy sphere 'is' a sphere. More precisely, one fixes a...
. Whether or not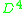
admits an exotic smooth structure is another open problem, closely linked to the Schoenflies problemSchönflies problemIn mathematics, the Schoenflies problem or Schoenflies theorem, of geometric topology is a sharpening of the Jordan curve theorem by Arthur Schoenflies.-Original formulation:...
in dimension four.
Mazur's Observation
Let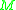 be the Mazur manifold, constructed as union a 2-handle. Here is a sketch of Mazur's argument that the doubleDouble (manifold)
In the subject of manifold theory in mathematics, if M is a manifold with boundary, its double is obtained by gluing two copies of M together along their common boundary...
of such a Mazur manifold is
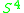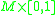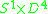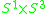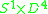. is a contractible 5-manifold constructed as union a 2-handle. The 2-handle can be unknotted since the attaching map is a framed knot in the 4-manifold . So union the 2-handle is diffeomorphic to 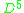. The boundary of is 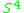. But the boundary of 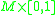is the doubleDouble (manifold)
In the subject of manifold theory in mathematics, if M is a manifold with boundary, its double is obtained by gluing two copies of M together along their common boundary...
of
.