Cohomology operation
Encyclopedia
In mathematics
, the cohomology operation concept became central to algebraic topology
, particularly homotopy theory, from the 1950s onwards, in the shape of the simple definition that if F is a functor
defining a cohomology theory, then a cohomology operation should be a natural transformation
from F to itself. Throughout there have been two basic points:
The origin of these studies was the work of Pontryagin, Postnikov, and Norman Steenrod
, who first defined the Pontryagin square, Postnikov square
, and Steenrod square operations for singular cohomology, in the case of mod 2 coefficients. The combinatorial aspect there arises as a formulation of the failure of a natural diagonal map, at cochain level. The general theory of the Steenrod algebra
of operations has been brought into close relation with that of the symmetric group
.
In the Adams spectral sequence
the bicommutant aspect is implicit in the use of Ext functor
s, the derived functor
s of Hom-functors; if there is a bicommutant aspect, taken over the Steenrod algebra acting, it is only at a derived level. The convergence is to groups in stable homotopy theory
, about which information is hard to come by. This connection established the deep interest of the cohomology operations for homotopy theory, and has been a research topic ever since. An extraordinary cohomology theory has its own cohomology operations, and these may exhibit a richer set on constraints.
of type
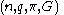
is a natural transformation
of functors
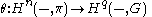
defined on CW complex
es.
by an Eilenberg-MacLane space
, so by the Yoneda lemma
a cohomology operation of type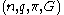
is given by a homotopy
class of maps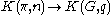
. Using representability
once again, the cohomology operation is given by an element of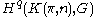
.
Symbolically, letting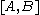
denote the set of homotopy classes of maps from 
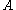to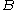 
,
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the cohomology operation concept became central to algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
, particularly homotopy theory, from the 1950s onwards, in the shape of the simple definition that if F is a functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
defining a cohomology theory, then a cohomology operation should be a natural transformation
Natural transformation
In category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Indeed this intuition...
from F to itself. Throughout there have been two basic points:
- the operations can be studied by combinatorial means; and
- the effect of the operations is to yield an interesting bicommutant theory.
The origin of these studies was the work of Pontryagin, Postnikov, and Norman Steenrod
Norman Steenrod
Norman Earl Steenrod was a preeminent mathematician most widely known for his contributions to the field of algebraic topology.-Life:...
, who first defined the Pontryagin square, Postnikov square
Postnikov square
In algebraic topology, a Postnikov square is a certain cohomology operation from a first cohomology group H1 to a third cohomology group H3, introduced by . described a generalization taking classes in Ht to H2t+1....
, and Steenrod square operations for singular cohomology, in the case of mod 2 coefficients. The combinatorial aspect there arises as a formulation of the failure of a natural diagonal map, at cochain level. The general theory of the Steenrod algebra
Steenrod algebra
In algebraic topology, a Steenrod algebra was defined by to be the algebra of stable cohomology operations for mod p cohomology.For a given prime number p, the Steenrod algebra Ap is the graded Hopf algebra over the field Fp of order p, consisting of all stable cohomology operations for mod p...
of operations has been brought into close relation with that of the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
.
In the Adams spectral sequence
Adams spectral sequence
In mathematics, the Adams spectral sequence is a spectral sequence introduced by . Like all spectral sequences, it is a computational tool; it relates homology theory to what is now called stable homotopy theory...
the bicommutant aspect is implicit in the use of Ext functor
Ext functor
In mathematics, the Ext functors of homological algebra are derived functors of Hom functors. They were first used in algebraic topology, but are common in many areas of mathematics.- Definition and computation :...
s, the derived functor
Derived functor
In mathematics, certain functors may be derived to obtain other functors closely related to the original ones. This operation, while fairly abstract, unifies a number of constructions throughout mathematics.- Motivation :...
s of Hom-functors; if there is a bicommutant aspect, taken over the Steenrod algebra acting, it is only at a derived level. The convergence is to groups in stable homotopy theory
Stable homotopy theory
In mathematics, stable homotopy theory is that part of homotopy theory concerned with all structure and phenomena that remain after sufficiently many applications of the suspension functor...
, about which information is hard to come by. This connection established the deep interest of the cohomology operations for homotopy theory, and has been a research topic ever since. An extraordinary cohomology theory has its own cohomology operations, and these may exhibit a richer set on constraints.
Formal definition
A cohomology operation of type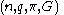is a natural transformation
Natural transformation
In category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Indeed this intuition...
of functors
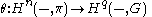
defined on CW complex
CW complex
In topology, a CW complex is a type of topological space introduced by J. H. C. Whitehead to meet the needs of homotopy theory. This class of spaces is broader and has some better categorical properties than simplicial complexes, but still retains a combinatorial naturethat allows for...
es.
Relation to Eilenberg-MacLane spaces
Cohomology of CW complexes is representableRepresentable functor
In mathematics, particularly category theory, a representable functor is a functor of a special form from an arbitrary category into the category of sets. Such functors give representations of an abstract category in terms of known structures In mathematics, particularly category theory, a...
by an Eilenberg-MacLane space
Eilenberg-MacLane space
In mathematics, an Eilenberg–MacLane spaceSaunders Mac Lane originally spelt his name "MacLane" , and co-published the papers establishing the notion of Eilenberg–MacLane spaces under this name. In mathematics, an Eilenberg–MacLane spaceSaunders Mac Lane originally spelt his name "MacLane" (without...
, so by the Yoneda lemma
Yoneda lemma
In mathematics, specifically in category theory, the Yoneda lemma is an abstract result on functors of the type morphisms into a fixed object. It is a vast generalisation of Cayley's theorem from group theory...
a cohomology operation of type
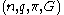is given by a homotopyHomotopy
In topology, two continuous functions from one topological space to another are called homotopic if one can be "continuously deformed" into the other, such a deformation being called a homotopy between the two functions...
class of maps
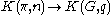. Using representabilityRepresentable functor
In mathematics, particularly category theory, a representable functor is a functor of a special form from an arbitrary category into the category of sets. Such functors give representations of an abstract category in terms of known structures In mathematics, particularly category theory, a...
once again, the cohomology operation is given by an element of
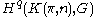.Symbolically, letting
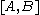denote the set of homotopy classes of maps from 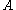to 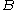,