
Differential graded algebra
Encyclopedia
In mathematics
, in particular abstract algebra
and topology
, a differential graded algebra is a graded algebra
with an added chain complex structure that respects the algebra structure.
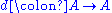 which is either degree 1 (cochain complex convention) or degree
which is either degree 1 (cochain complex convention) or degree 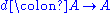 (chain complex convention) that satisfies two conditions:
(chain complex convention) that satisfies two conditions:

Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in particular abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
and topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, a differential graded algebra is a graded algebra
Graded algebra
In mathematics, in particular abstract algebra, a graded algebra is an algebra over a field with an extra piece of structure, known as a gradation ....
with an added chain complex structure that respects the algebra structure.
Definition
A differential graded algebra (or simply DGA) A is a graded algebra equipped with a map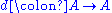 which is either degree 1 (cochain complex convention) or degree
which is either degree 1 (cochain complex convention) or degree 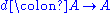 (chain complex convention) that satisfies two conditions:
(chain complex convention) that satisfies two conditions:
- This says that d gives A the structure of a chain complexChain complexIn mathematics, chain complex and cochain complex are constructs originally used in the field of algebraic topology. They are algebraic means of representing the relationships between the cycles and boundaries in various dimensions of some "space". Here the "space" could be a topological space or...
or cochain complex (accordingly as the differential reduces or raises degree).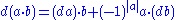 .
. - This says that the differentialDifferential (mathematics)In mathematics, the term differential has several meanings.-Basic notions:* In calculus, the differential represents a change in the linearization of a function....
d respects the graded Leibniz rule.
Examples of DGAs
- The Koszul complexKoszul complexIn mathematics, the Koszul complex was first introduced to define a cohomology theory for Lie algebras, by Jean-Louis Koszul...
is a DGA. - The Tensor algebraTensor algebraIn mathematics, the tensor algebra of a vector space V, denoted T or T•, is the algebra of tensors on V with multiplication being the tensor product...
is a DGA with differential similar to that of the Koszul complex. - The Singular cohomology with coefficients in a ring is a DGA; the differential is given by the Bockstein homomorphismBockstein homomorphismIn homological algebra, the Bockstein homomorphism, introduced by , is a connecting homomorphism associated with a short exact sequenceof abelian groups, when they are introduced as coefficients into a chain complex C, and which appears in the homology groups as a homomorphism reducing degree by...
, and the product given by the cup productCup productIn mathematics, specifically in algebraic topology, the cup product is a method of adjoining two cocycles of degree p and q to form a composite cocycle of degree p + q. This defines an associative graded commutative product operation in cohomology, turning the cohomology of a space X into a...
. - Differential forms on a manifoldManifoldIn mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
, together with the exterior derivation and the wedge-product form a DGA.
Other facts about DGAs
- The homologyHomology (mathematics)In mathematics , homology is a certain general procedure to associate a sequence of abelian groups or modules with a given mathematical object such as a topological space or a group...
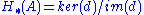 of a DGA
of a DGA  is a graded ring.
is a graded ring.

