Källén-Lehmann spectral representation
Encyclopedia
Källén-Lehmann spectral representation gives a general expression for the two-point function
of an interacting quantum field theory
as a sum of free propagators. It was discovered by Gunnar Källén
and Harry Lehmann
independently. This can be written as
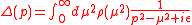
being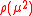
the spectral density function that should be positive definite. In a gauge theory
, this latter condition cannot be granted but nevertheless a spectral representation can be provided. This belongs to non-perturbative techniques of quantum field theory
.
, one consider a complete set of states 
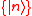so that, for the two-point function
one can write
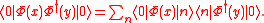
We can now use Poincaré invariance
of the vacuum to write down
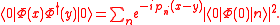
Let us introduce the spectral density function
.
We have used the fact that our two-point function, being a function of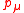
, can only depend on 
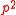. Besides, all the intermediate states have 
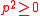and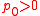 
. It is immediate to realize that the spectral density function is real and positive. So, one can write
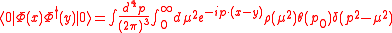
and we freely interchange the integration, this should be done carefully from a mathematical standpoint but here we ignore this, and write this expression as
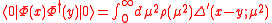
being
.
From CPT theorem
we also know that holds an identical expression for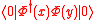
and so we arrive at the expression for the cronologically ordered product of fields
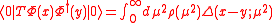
being now
a free particle propagator
. Now, as we have the exact propagator given by the chronologically ordered two-point function, we have obtained the spectral decomposition.
Correlation function (quantum field theory)
In quantum field theory, the matrix element computed by inserting a product of operators between two states, usually the vacuum states, is called a correlation function....
of an interacting quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
as a sum of free propagators. It was discovered by Gunnar Källén
Gunnar Källén
Gunnar Källén, born February 13, 1926 in Kristianstad, Sweden and died October 13, 1968 in Hannover, Germany in a plane accident. Källén was a leading Swedish theoretical physicist and a professor at Lund University until his death at the age of 42....
and Harry Lehmann
Harry Lehmann
Harry Lehmann was a German physicist.Lehmann studied physics at Rostock and the Humboldt-Universität zu Berlin....
independently. This can be written as
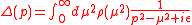
being
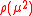the spectral density function that should be positive definite. In a gauge theoryGauge theory
In physics, gauge invariance is the property of a field theory in which different configurations of the underlying fundamental but unobservable fields result in identical observable quantities. A theory with such a property is called a gauge theory...
, this latter condition cannot be granted but nevertheless a spectral representation can be provided. This belongs to non-perturbative techniques of quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
.
Mathematical derivation
In order to derive a spectral representation for the propagator of a field, one consider a complete set of states 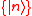so that, for the two-point functionCorrelation function (quantum field theory)
In quantum field theory, the matrix element computed by inserting a product of operators between two states, usually the vacuum states, is called a correlation function....
one can write
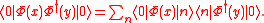
We can now use Poincaré invariance
Poincaré group
In physics and mathematics, the Poincaré group, named after Henri Poincaré, is the group of isometries of Minkowski spacetime.-Simple explanation:...
of the vacuum to write down
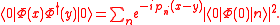
Let us introduce the spectral density function
.We have used the fact that our two-point function, being a function of
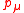, can only depend on 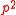. Besides, all the intermediate states have 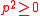and 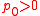. It is immediate to realize that the spectral density function is real and positive. So, one can write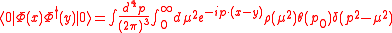and we freely interchange the integration, this should be done carefully from a mathematical standpoint but here we ignore this, and write this expression as
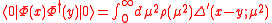
being
.From CPT theorem
CPT theorem
In quantum field theory the CPT theorem states that any canonical quantum field theory is invariant under the CPT operation, which is a combination of three discrete transformations: charge conjugation C, parity transformation P, and time reversal T...
we also know that holds an identical expression for
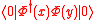and so we arrive at the expression for the cronologically ordered product of fields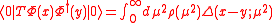being now
a free particle propagator
Propagator
In quantum mechanics and quantum field theory, the propagator gives the probability amplitude for a particle to travel from one place to another in a given time, or to travel with a certain energy and momentum. Propagators are used to represent the contribution of virtual particles on the internal...
. Now, as we have the exact propagator given by the chronologically ordered two-point function, we have obtained the spectral decomposition.
External links
See also
- Quantum field theoryQuantum field theoryQuantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
- Correlation functionsCorrelation function (quantum field theory)In quantum field theory, the matrix element computed by inserting a product of operators between two states, usually the vacuum states, is called a correlation function....
- PropagatorPropagatorIn quantum mechanics and quantum field theory, the propagator gives the probability amplitude for a particle to travel from one place to another in a given time, or to travel with a certain energy and momentum. Propagators are used to represent the contribution of virtual particles on the internal...