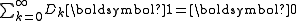Markovian arrival processes
Encyclopedia
In queueing theory
, Markovian arrival processes are used to model the arrival of customers to a queue.
Some of the most common include the Poisson process, Markov arrival process and the batch Markov arrival process.
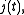a Markov process which is generated by a generator or rate matrix, 
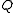. The other process is a counting process 
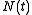, which has state space 
(where 
is the set of all natural numbers).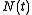 
increases every time there is a transition in 
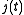that is marked.
counts the number of arrivals, each of which has an exponentially distributed
time between arrival. In the most general case this can be represented by the rate matrix,
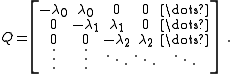
In the homogeneous case this is more simply,
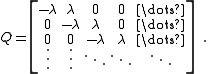
Here every transition is marked.
sojourn between arrivals. The homogeneous case has rate matrix,
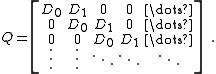
An arrival is seen every time a transition occurs that increases the level (a marked transition), e.g. a transition in the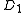
sub-matrix
.
Sub-matrices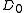
and 
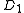have elements of 
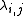, the rate of a Poisson process
, such that,
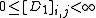
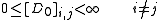
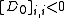
and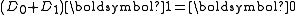
There are several special cases of the Markov arrival process.
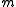Poisson processes are switched between by an underlying Markov process. If each of the 
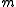Poisson processes has rate 
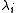and the underlying process is generated by a 
generator matrix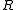 
, then in the MAP representation,
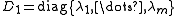
a diagonal matrix
of the rates of the Poisson process, and
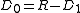
sojourn between arrivals. For example if an arrival process has an interarrival time distribution PH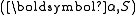
with an exit vector denoted 
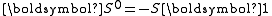, the arrival process has generator matrix,
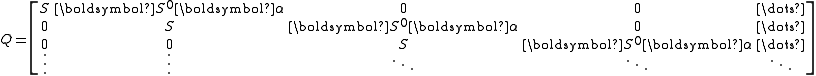
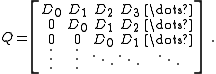
An arrival of size
occurs every time a transition occurs in the sub-matrix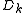 
. Sub-matrices 
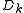have elements of 
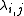, the rate of a Poisson process
, such that,
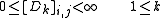
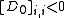
and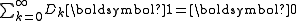
Queueing theory
Queueing theory is the mathematical study of waiting lines, or queues. The theory enables mathematical analysis of several related processes, including arriving at the queue, waiting in the queue , and being served at the front of the queue...
, Markovian arrival processes are used to model the arrival of customers to a queue.
Some of the most common include the Poisson process, Markov arrival process and the batch Markov arrival process.
Background
Markovian arrival processes have two processes. A continuous-time Markov process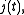 a Markov process which is generated by a generator or rate matrix, 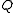. The other process is a counting process 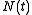, which has state space (where is the set of all natural numbers). 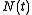increases every time there is a transition in 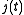that is marked.Poisson process
The Poisson arrival process or Poisson processPoisson process
A Poisson process, named after the French mathematician Siméon-Denis Poisson , is a stochastic process in which events occur continuously and independently of one another...
counts the number of arrivals, each of which has an exponentially distributed
Exponential distribution
In probability theory and statistics, the exponential distribution is a family of continuous probability distributions. It describes the time between events in a Poisson process, i.e...
time between arrival. In the most general case this can be represented by the rate matrix,
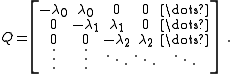
In the homogeneous case this is more simply,
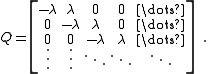
Here every transition is marked.
Markov arrival process
The Markov arrival process (MAP) is a generalization of the Poisson process by having non-exponential distributionExponential distribution
In probability theory and statistics, the exponential distribution is a family of continuous probability distributions. It describes the time between events in a Poisson process, i.e...
sojourn between arrivals. The homogeneous case has rate matrix,
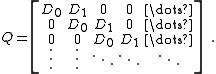
An arrival is seen every time a transition occurs that increases the level (a marked transition), e.g. a transition in the
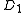sub-matrixMatrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
.
Sub-matrices
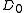and 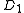have elements of 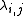, the rate of a Poisson processPoisson process
A Poisson process, named after the French mathematician Siméon-Denis Poisson , is a stochastic process in which events occur continuously and independently of one another...
, such that,
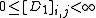
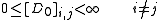
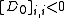
and
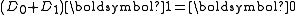
There are several special cases of the Markov arrival process.
Markov-modulated Poisson process
The Markov-modulated Poisson process or MMPP where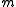 Poisson processes are switched between by an underlying Markov process. If each of the 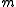Poisson processes has rate 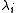and the underlying process is generated by a generator matrix 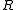, then in the MAP representation,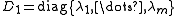a diagonal matrix
Diagonal matrix
In linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...
of the rates of the Poisson process, and
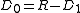
Phase-type renewal process
The phase-type renewal process is a Markov arrival process with phase-type distributedPhase-type distribution
A phase-type distribution is a probability distribution that results from a system of one or more inter-related Poisson processes occurring in sequence, or phases. The sequence in which each of the phases occur may itself be a stochastic process. The distribution can be represented by a random...
sojourn between arrivals. For example if an arrival process has an interarrival time distribution PH
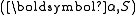with an exit vector denoted 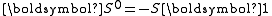, the arrival process has generator matrix,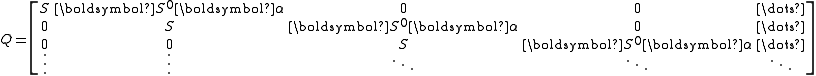Batch Markov arrival process
The batch Markovian arrival process (BMAP) is a generalisation of the Markovian arrival process by having arrivals of size greater than one. The homogeneous case has rate matrix,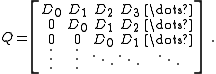An arrival of size
occurs every time a transition occurs in the sub-matrix 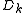. Sub-matrices 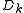have elements of 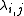, the rate of a Poisson processPoisson process
A Poisson process, named after the French mathematician Siméon-Denis Poisson , is a stochastic process in which events occur continuously and independently of one another...
, such that,
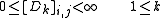
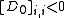
and