Magnetohydrodynamic turbulence
Encyclopedia
Magnetohydrodynamics
(MHD) deals with what is a quasi-neutral fluid with very high conductivity. The fluid approximation implies that the we focus at macro length and time scales which are much larger than the collision length and collision time respectively. In this article we will discuss MHD turbulence which is observed when the Reynolds number of the magnetofluid is large.
where u, B, p represent the velocity, magnetic, and total pressure (thermal+magnetic) fields,
and 
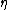represent kinematic viscosity and magnetic diffusivity. The third equation is the incompressibility condition
. In the above equation, the magnetic field
is in Alfvén units (same as velocity units).
The total magnetic field can be split into two parts: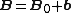
(mean + fluctuations).
The above equations in terms of Elsässer variables (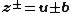
) are
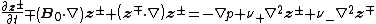
where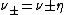
. Nonlinear interactions occur between the Alfvénic fluctuations 
.
The important nondimensional parameters for MHD are
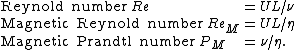
The magnetic Prandtl number
is an important property of the fluid. Liquid metals have small magnetic Prandtl numbers, for example, liquid sodium's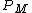
is around 
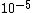. But plasmas have large 
.
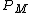The Reynolds number is the ratio of the nonlinear term
of the Navier-Stokes equation to the viscous term. While the magnetic Reynolds number is the ratio of the nonlinear term and the diffusive term of the induction equation.
In many practical situations, the Reynolds number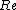
of the flow is quite large. For such flows typically the velocity and the magnetic fields are random. Such flows are called to exhibit MHD turbulence. Note that 
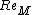need not be large for MHD turbulence. 
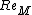plays an important role in dynamo (magnetic field generation) problem.
The mean magnetic field plays an important role in MHD turbulence, for example it can make the turbulence anisotropic; suppress the turbulence by decreasing energy cascade etc. The earlier MHD turbulence models assumed isotropy of turbulence, while the later models have studied anisotropic aspects. In the following discussions will summarize these models. More discussions on MHD turbulence can be found in Biskamp and Verma.
of a strong mean magnetic field,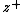
and 
wavepackets travel in opposite directions with
the phase velocity of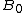
, and interact weakly. The relevant time scale is Alfven time 
. As a results the energy spectra is
E^u(k) \approx E^b(k) \approx A (\Pi V_A)^{1/2} k^{-3/2}.
where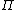
is the energy cascade rate.
Later Dobrowolny et al. derived the following generalized formulas for the cascade rates of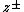
variables:
\Pi^+ \approx \Pi^{-} \approx \tau^{\pm}_k E^{+}(k) E^{-}(k) k^4 \approx E^{+}(k) E^{-}(k) k^3 / B_0
where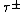
are the interaction time scales of 
variables.
Iroshnikov and Kraichnan's phenomenology follows once we choose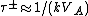
.
Marsch chose the nonlinear time scale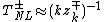
as the interaction time scale for the eddies and derived Kolmogorov-like energy spectrum for the Elsasser variables:
E^{\pm}(k) = K^{\pm} (\Pi^{\pm})^{4/3} (\Pi^{\mp})^{-2/3} k^{-5/3}
where
and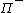 
are the energy cascade rates of 
and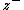 
respectively, and 
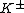are constants.
Matthaeus and Zhou attempted to combine the above two time scales by postulating the interaction time to be the harmonic
mean of Alfven time and nonlinear time.
The main difference between the two competing phenomenologies (-3/2 and -5/3) is the chosen time scales for the interaction time.
The main underlying assumption in that Iroshnikov and Kraichnan's phenomenology should work for strong mean magnetic field,
whereas Marsh's phenomenology should work when the fluctuations dominate the mean magnetic field (strong turbulence).
However, as we will discuss below, the solar wind observations and numerical simulations tend to favour -5/3 energy spectrum
even when the mean magnetic field is stronger compared to the fluctuations. This issue was resolved by Verma using renormalization
group analysis by showing that the Alfvénic fluctuations are affected by scale-dependent "local mean magnetic field". The local mean magnetic field scales as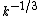
, substitution of which in Dobrowolny's equation yields Kolmogorov's energy spectrum for MHD turbulence.
Renormalization group analysis have been also performed for computing the renormalized viscosity and resistivity. It was shown that these diffusive quantities scale as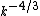
that again yields 
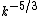energy spectra consistent with Kolmogorov-like model for MHD turbulence. The above renormalization group calculation has been performed for both zero and nonzero cross helicity.
The above phenomenologies assume isotropic turbulence that is not the case in the presence of a mean magnetic field. The mean magnetic field typically suppresses the energy cascade along the direction of the mean magnetic field.
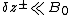, Galtier et al. showed using kinetic equations that
where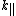
and 
are components of the wavenumber parallel and perpendicular to mean magnetic field. The above limit is called the weak turbulence limit.
Under the strong turbulence limit,
, Goldereich and Sridhar argue that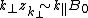 
("critical balanced state") which implies that
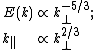
The above anisotropic turbulence phenomenology has been extended for large cross helicity MHD.
collected from the spacecrafts. The kinetic and magnetic energy spectra, as well as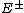
are closer to
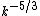compared to 
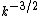, thus favoring Kolmogorov-like phenomenology for MHD
turbulence . The interplanetary and interstellar electron density fluctuations also provide
a window for investigating MHD turbulence.
Energy fluxes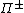
can be more reliable quantities to validate MHD turbulence models.
When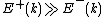
(high cross helicity fluid or imbalanced MHD) the energy flux predictions of Kraichnan and Iroshnikov model is very different from that of Kolmogorov-like model. It has been shown using DNS that the fluxes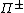
computed from the numerical simulations are in better agreement with Kolmogorov-like model compared to Kraichnan and Iroshnikov model.
Anisotropic aspects of MHD turbulence have also been studied using numerical simulations. The predictions of Goldreich and Sridhar (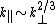
) have been verified in many simulations. Some of the recent simulations report dynamic alignment of velocity and magnetic field fluctuations in the inertial range, and 
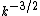energy spectra.
have been computed both theoretically and numerically. These calculations show a significant energy transfer from the
large scale velocity field to the large scale magnetic field. Also, the cascade of magnetic energy is typically forward. These results have critical
bearing on dynamo problem.
----
There are many open challenges in this field that hopefully will be resolved in near future with the help of numerical simulations, theoretical modelling, experiments, and observations (e.g., solar wind).
Magnetohydrodynamics
Magnetohydrodynamics is an academic discipline which studies the dynamics of electrically conducting fluids. Examples of such fluids include plasmas, liquid metals, and salt water or electrolytes...
(MHD) deals with what is a quasi-neutral fluid with very high conductivity. The fluid approximation implies that the we focus at macro length and time scales which are much larger than the collision length and collision time respectively. In this article we will discuss MHD turbulence which is observed when the Reynolds number of the magnetofluid is large.
Incompressible MHD equations
The incompressible MHD equations arewhere u, B, p represent the velocity, magnetic, and total pressure (thermal+magnetic) fields,
and 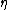represent kinematic viscosity and magnetic diffusivity. The third equation is the incompressibility conditionIncompressible flow
In fluid mechanics or more generally continuum mechanics, incompressible flow refers to flow in which the material density is constant within an infinitesimal volume that moves with the velocity of the fluid...
. In the above equation, the magnetic field
Magnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
is in Alfvén units (same as velocity units).
The total magnetic field can be split into two parts:
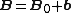(mean + fluctuations).The above equations in terms of Elsässer variables (
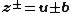) are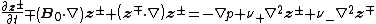where
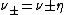. Nonlinear interactions occur between the Alfvénic fluctuations .The important nondimensional parameters for MHD are
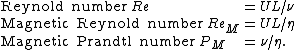
The magnetic Prandtl number
Magnetic Prandtl number
The Magnetic Prandtl number is a dimensionless quantity occurring in magnetohydrodynamics which approximates the ratio of momentum diffusivity and magnetic diffusivity...
is an important property of the fluid. Liquid metals have small magnetic Prandtl numbers, for example, liquid sodium's
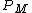is around 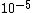. But plasmas have large 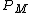.The Reynolds number is the ratio of the nonlinear term
of the Navier-Stokes equation to the viscous term. While the magnetic Reynolds number is the ratio of the nonlinear term and the diffusive term of the induction equation.In many practical situations, the Reynolds number
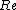of the flow is quite large. For such flows typically the velocity and the magnetic fields are random. Such flows are called to exhibit MHD turbulence. Note that 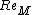need not be large for MHD turbulence. 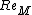plays an important role in dynamo (magnetic field generation) problem.The mean magnetic field plays an important role in MHD turbulence, for example it can make the turbulence anisotropic; suppress the turbulence by decreasing energy cascade etc. The earlier MHD turbulence models assumed isotropy of turbulence, while the later models have studied anisotropic aspects. In the following discussions will summarize these models. More discussions on MHD turbulence can be found in Biskamp and Verma.
Isotropic models
Iroshnikov and Kraichnan formulated the first phenomenological theory of MHD turbulence. They argued that in the presenceof a strong mean magnetic field,
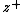and wavepackets travel in opposite directions withthe phase velocity of
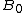, and interact weakly. The relevant time scale is Alfven time . As a results the energy spectra isE^u(k) \approx E^b(k) \approx A (\Pi V_A)^{1/2} k^{-3/2}.
where
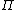is the energy cascade rate.Later Dobrowolny et al. derived the following generalized formulas for the cascade rates of
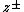variables:
\Pi^+ \approx \Pi^{-} \approx \tau^{\pm}_k E^{+}(k) E^{-}(k) k^4 \approx E^{+}(k) E^{-}(k) k^3 / B_0
where
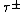are the interaction time scales of variables.Iroshnikov and Kraichnan's phenomenology follows once we choose
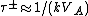.Marsch chose the nonlinear time scale
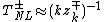as the interaction time scale for the eddies and derived Kolmogorov-like energy spectrum for the Elsasser variables:
E^{\pm}(k) = K^{\pm} (\Pi^{\pm})^{4/3} (\Pi^{\mp})^{-2/3} k^{-5/3}
where
and 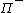are the energy cascade rates of and 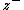respectively, and 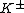are constants.Matthaeus and Zhou attempted to combine the above two time scales by postulating the interaction time to be the harmonic
mean of Alfven time and nonlinear time.
The main difference between the two competing phenomenologies (-3/2 and -5/3) is the chosen time scales for the interaction time.
The main underlying assumption in that Iroshnikov and Kraichnan's phenomenology should work for strong mean magnetic field,
whereas Marsh's phenomenology should work when the fluctuations dominate the mean magnetic field (strong turbulence).
However, as we will discuss below, the solar wind observations and numerical simulations tend to favour -5/3 energy spectrum
even when the mean magnetic field is stronger compared to the fluctuations. This issue was resolved by Verma using renormalization
Renormalization
In quantum field theory, the statistical mechanics of fields, and the theory of self-similar geometric structures, renormalization is any of a collection of techniques used to treat infinities arising in calculated quantities....
group analysis by showing that the Alfvénic fluctuations are affected by scale-dependent "local mean magnetic field". The local mean magnetic field scales as
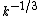, substitution of which in Dobrowolny's equation yields Kolmogorov's energy spectrum for MHD turbulence.Renormalization group analysis have been also performed for computing the renormalized viscosity and resistivity. It was shown that these diffusive quantities scale as
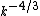that again yields 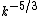energy spectra consistent with Kolmogorov-like model for MHD turbulence. The above renormalization group calculation has been performed for both zero and nonzero cross helicity.The above phenomenologies assume isotropic turbulence that is not the case in the presence of a mean magnetic field. The mean magnetic field typically suppresses the energy cascade along the direction of the mean magnetic field.
Anisotropic models
Mean magnetic field makes turbulence anisotropic. This aspect has been studied in last two decades. In the limit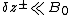, Galtier et al. showed using kinetic equations thatwhere
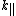and are components of the wavenumber parallel and perpendicular to mean magnetic field. The above limit is called the weak turbulence limit.Under the strong turbulence limit,
, Goldereich and Sridhar argue that 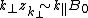("critical balanced state") which implies that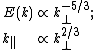The above anisotropic turbulence phenomenology has been extended for large cross helicity MHD.
Solar wind observations
Solar wind plasma is in turbulent state. Researchers have calculated the energy spectra of the solar wind plasma from the datacollected from the spacecrafts. The kinetic and magnetic energy spectra, as well as
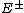are closer to 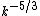compared to 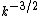, thus favoring Kolmogorov-like phenomenology for MHDturbulence . The interplanetary and interstellar electron density fluctuations also provide
a window for investigating MHD turbulence.
Numerical simulations
The theoretical models discussed above are tested using the high resolution direct numerical simulation (DNS). Number of recent simulations report the spectral indices to be closer to 5/3. There are others that report the spectral indices near 3/2. The regime of power law is typically less than a decade. Since 5/3 and 3/2 are quite close numerically, it is quite difficult to ascertain the validity of MHD turbulence models from the energy spectra.Energy fluxes
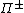can be more reliable quantities to validate MHD turbulence models.When
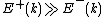
(high cross helicity fluid or imbalanced MHD) the energy flux predictions of Kraichnan and Iroshnikov model is very different from that of Kolmogorov-like model. It has been shown using DNS that the fluxes
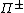computed from the numerical simulations are in better agreement with Kolmogorov-like model compared to Kraichnan and Iroshnikov model.Anisotropic aspects of MHD turbulence have also been studied using numerical simulations. The predictions of Goldreich and Sridhar (
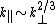) have been verified in many simulations. Some of the recent simulations report dynamic alignment of velocity and magnetic field fluctuations in the inertial range, and 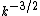energy spectra.Energy transfer
Energy transfer among various scales between the velocity and magnetic field is an important problem in MHD turbulence. These quantitieshave been computed both theoretically and numerically. These calculations show a significant energy transfer from the
large scale velocity field to the large scale magnetic field. Also, the cascade of magnetic energy is typically forward. These results have critical
bearing on dynamo problem.
----
There are many open challenges in this field that hopefully will be resolved in near future with the help of numerical simulations, theoretical modelling, experiments, and observations (e.g., solar wind).
See also
- MagnetohydrodynamicsMagnetohydrodynamicsMagnetohydrodynamics is an academic discipline which studies the dynamics of electrically conducting fluids. Examples of such fluids include plasmas, liquid metals, and salt water or electrolytes...
- TurbulenceTurbulenceIn fluid dynamics, turbulence or turbulent flow is a flow regime characterized by chaotic and stochastic property changes. This includes low momentum diffusion, high momentum convection, and rapid variation of pressure and velocity in space and time...
- Alfvén waveAlfvén waveAn Alfvén wave, named after Hannes Alfvén, is a type of magnetohydrodynamic wave.-Definition:An Alfvén wave in a plasma is a low-frequency travelling oscillation of the ions and the magnetic field...
- Solar dynamoSolar dynamoThe solar dynamo is the physical process that generates the Sun's magnetic field. The Sun is permeated by an overall dipole magnetic field, as are many other celestial bodies such as the Earth. The dipole field is produced by a circular electric current flowing deep within the star, following...
- Reynolds number
- Navier–Stokes equations
- Computational magnetohydrodynamicsComputational MagnetohydrodynamicsComputational magnetohydrodynamics is a rapidly developing branch of magnetohydrodynamics that uses numerical methods and algorithms to solve and analyze problems that involve electrically conducting fluids. Most of the methods used in CMHD are borrowed from the well established techniques...
- Computational fluid dynamicsComputational fluid dynamicsComputational fluid dynamics, usually abbreviated as CFD, is a branch of fluid mechanics that uses numerical methods and algorithms to solve and analyze problems that involve fluid flows. Computers are used to perform the calculations required to simulate the interaction of liquids and gases with...
- Solar windSolar windThe solar wind is a stream of charged particles ejected from the upper atmosphere of the Sun. It mostly consists of electrons and protons with energies usually between 1.5 and 10 keV. The stream of particles varies in temperature and speed over time...
- Magnetic flow meterMagnetic flow meterThe third most common flowmeter behind differential pressure and positive displacement flow meters, is the magnetic flow meter, also technically an electromagnetic flow meter or more commonly just called a mag meter. A magnetic field is applied to the metering tube, which results in a potential...
- Ionic liquidIonic liquidAn ionic liquid is a salt in the liquid state. In some contexts, the term has been restricted to salts whose melting point is below some arbitrary temperature, such as . While ordinary liquids such as water and gasoline are predominantly made of electrically neutral molecules, ILs are largely made...