Lubin–Tate formal group law
Encyclopedia
In mathematics, the Lubin–Tate formal group law is a formal group law introduced by to isolate the local field
part of the classical theory of complex multiplication
of elliptic function
s. It does this by considering the (formal) endomorphism
s of the formal group, emulating the way in which elliptic curve
s with extra endomorphisms are used to give abelian extensions of global field
s
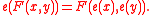
More generally, the choice for e may be any power series such that
All such group laws, for different choices of e satisfying these conditions, are strictly isomorphic. We choose these conditions so as to ensure that they reduce modulo the maximal ideal to Frobenius and the derivative at the origin is the prime element.
For each element a in Zp there is a unique endomorphism f of the Lubin–Tate formal group law such that f(x) = ax + higher-degree terms. This gives an action of the ring Zp on the Lubin–Tate formal group law.
There is a similar construction with Zp replaced by any complete discrete valuation ring
with finite residue class field, where p is replaced by a choice of uniformizer.
, which is of huge importance in class field theory
, generating the maximal unramified extension
as the image of the reciprocity map.
For this example we need the notion of an endomorphism of formal groups, which is a formal group homomorphism f, in which the domain is the codomain. A formal group homomorphism from a formal group F to a formal group G is a power series over the same ring as the formal groups which has zero constant term and is such that:
Consider a formal group F(X,Y) with coefficients in the ring of integers in a local field (for example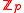
), taking X and Y to be in the unique maximal ideal gives us a convergent power series and in this case we define 
and we have a genuine group law. For example if 
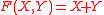, then this is the usual addition. This is isomorphic to the case of 
, where we have multiplication on the set of elements which can be written as 1 added to an element of the prime ideal. In the latter case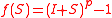 
is an endomorphism of F and the isomorphism identifies f with the Frobenius element.
of such formal groups. A later application of the theory has been in the field of stable homotopy theory
, with the construction of a particular extraordinary cohomology theory associated to the construction for a given prime p. As part of general machinery for formal groups, a cohomology theory with spectrum
is set up for the Lubin–Tate formal group, which also goes by the names of Morava E-theory or completed Johnson–Wilson theory
.
Local field
In mathematics, a local field is a special type of field that is a locally compact topological field with respect to a non-discrete topology.Given such a field, an absolute value can be defined on it. There are two basic types of local field: those in which the absolute value is archimedean and...
part of the classical theory of complex multiplication
Complex multiplication
In mathematics, complex multiplication is the theory of elliptic curves E that have an endomorphism ring larger than the integers; and also the theory in higher dimensions of abelian varieties A having enough endomorphisms in a certain precise sense In mathematics, complex multiplication is the...
of elliptic function
Elliptic function
In complex analysis, an elliptic function is a function defined on the complex plane that is periodic in two directions and at the same time is meromorphic...
s. It does this by considering the (formal) endomorphism
Endomorphism
In mathematics, an endomorphism is a morphism from a mathematical object to itself. For example, an endomorphism of a vector space V is a linear map ƒ: V → V, and an endomorphism of a group G is a group homomorphism ƒ: G → G. In general, we can talk about...
s of the formal group, emulating the way in which elliptic curve
Elliptic curve
In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
s with extra endomorphisms are used to give abelian extensions of global field
Global field
In mathematics, the term global field refers to either of the following:*an algebraic number field, i.e., a finite extension of Q, or*a global function field, i.e., the function field of an algebraic curve over a finite field, equivalently, a finite extension of Fq, the field of rational functions...
s
Definition of formal groups
Let Zp be the ring of p-adic integers. The Lubin–Tate formal group law is the unique (1-dimensional) formal group law F such that e(x) = px + xp is an endomorphism of F, in other words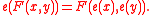More generally, the choice for e may be any power series such that
- e(x) = px + higher-degree terms and
- e(x) = xp mod p.
All such group laws, for different choices of e satisfying these conditions, are strictly isomorphic. We choose these conditions so as to ensure that they reduce modulo the maximal ideal to Frobenius and the derivative at the origin is the prime element.
For each element a in Zp there is a unique endomorphism f of the Lubin–Tate formal group law such that f(x) = ax + higher-degree terms. This gives an action of the ring Zp on the Lubin–Tate formal group law.
There is a similar construction with Zp replaced by any complete discrete valuation ring
Discrete valuation ring
In abstract algebra, a discrete valuation ring is a principal ideal domain with exactly one non-zero maximal ideal.This means a DVR is an integral domain R which satisfies any one of the following equivalent conditions:...
with finite residue class field, where p is replaced by a choice of uniformizer.
Example
We outline here a formal group equivalent of the Frobenius elementFrobenius endomorphism
In commutative algebra and field theory, the Frobenius endomorphism is a special endomorphism of commutative rings with prime characteristic p, an important class which includes finite fields. The endomorphism maps every element to its pth power...
, which is of huge importance in class field theory
Class field theory
In mathematics, class field theory is a major branch of algebraic number theory that studies abelian extensions of number fields.Most of the central results in this area were proved in the period between 1900 and 1950...
, generating the maximal unramified extension
Hilbert class field
In algebraic number theory, the Hilbert class field E of a number field K is the maximal abelian unramified extension of K. Its degree over K equals the class number of K and the Galois group of E over K is canonically isomorphic to the ideal class group of K using Frobenius elements for prime...
as the image of the reciprocity map.
For this example we need the notion of an endomorphism of formal groups, which is a formal group homomorphism f, in which the domain is the codomain. A formal group homomorphism from a formal group F to a formal group G is a power series over the same ring as the formal groups which has zero constant term and is such that:
Consider a formal group F(X,Y) with coefficients in the ring of integers in a local field (for example
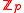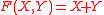), taking X and Y to be in the unique maximal ideal gives us a convergent power series and in this case we define and we have a genuine group law. For example if , then this is the usual addition. This is isomorphic to the case of , where we have multiplication on the set of elements which can be written as 1 added to an element of the prime ideal. In the latter case 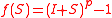is an endomorphism of F and the isomorphism identifies f with the Frobenius element.Generating ramified extensions
Lubin–Tate theory is important in explicit local class field theory. The unramified extension of any abelian extension is easily constructed, Lubin–Tate finds its value in producing the ramified part. This works by defining a family of modules (indexed by the natural numbers) over the ring of integers consisting of what can be considered as roots of the power series repeatedly composed with itself. The compositum of all fields formed by adjoining such modules to the original field gives the ramified part.Connection with stable homotopy theory
Lubin and Tate studied the deformation theoryDeformation theory
In mathematics, deformation theory is the study of infinitesimal conditions associated with varying a solution P of a problem to slightly different solutions Pε, where ε is a small number, or vector of small quantities. The infinitesimal conditions are therefore the result of applying the approach...
of such formal groups. A later application of the theory has been in the field of stable homotopy theory
Stable homotopy theory
In mathematics, stable homotopy theory is that part of homotopy theory concerned with all structure and phenomena that remain after sufficiently many applications of the suspension functor...
, with the construction of a particular extraordinary cohomology theory associated to the construction for a given prime p. As part of general machinery for formal groups, a cohomology theory with spectrum
Spectrum (homotopy theory)
In algebraic topology, a branch of mathematics, a spectrum is an object representing a generalized cohomology theory. There are several different constructions of categories of spectra, any of which gives a context for the same stable homotopy theory....
is set up for the Lubin–Tate formal group, which also goes by the names of Morava E-theory or completed Johnson–Wilson theory
Johnson–Wilson theory
In algebraic topology, Johnson–Wilson theory E is a generalized cohomology theory introduced by . Real Johnson–Wilson theory ER was introduced by ....
.